Introducción¶
Introducción¶
Aprender sobre visualización es importante por varias razones:
Comunicar información compleja de manera clara y efectiva: Al presentar datos de una manera visual, es más fácil identificar patrones y tendencias, así como también hacer comparaciones y contrastes. Esto es especialmente importante cuando se trabaja con grandes conjuntos de datos o cuando se trata de presentar información a un público diverso.
Descubrir información oculta o desconocida: A menudo, los datos pueden contener patrones o relaciones que no son obvios a simple vista, pero que pueden ser descubiertos mediante la exploración y la visualización. La visualización también puede ayudar a identificar errores y anomalías en los datos, lo que puede ser importante para la toma de decisiones y la planificación.
Mejorar la capacidad de análisis de datos: Al comprender cómo presentar datos de manera efectiva, se puede desarrollar una mejor comprensión de los datos y las relaciones que existen entre ellos. Esto puede ayudar a tomar decisiones informadas basadas en datos y a identificar tendencias y oportunidades que de otra manera podrían haber pasado desapercibidas.
Malos Gráficos¶

Buenos Gráficos¶
Primeras visualizaciones¶
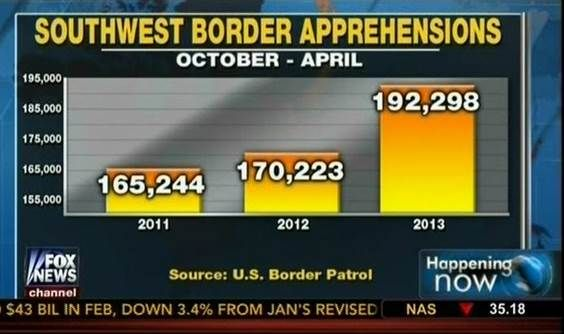
Campaña de Napoleón a Moscú (Charles Minard, 1889)
Gráfico que muestra el número de las fuerzas francesas en su marcha hacia Moscú y durante la retirada, por Charles Minard. También contiene información ambiental como la temperatura por fecha.

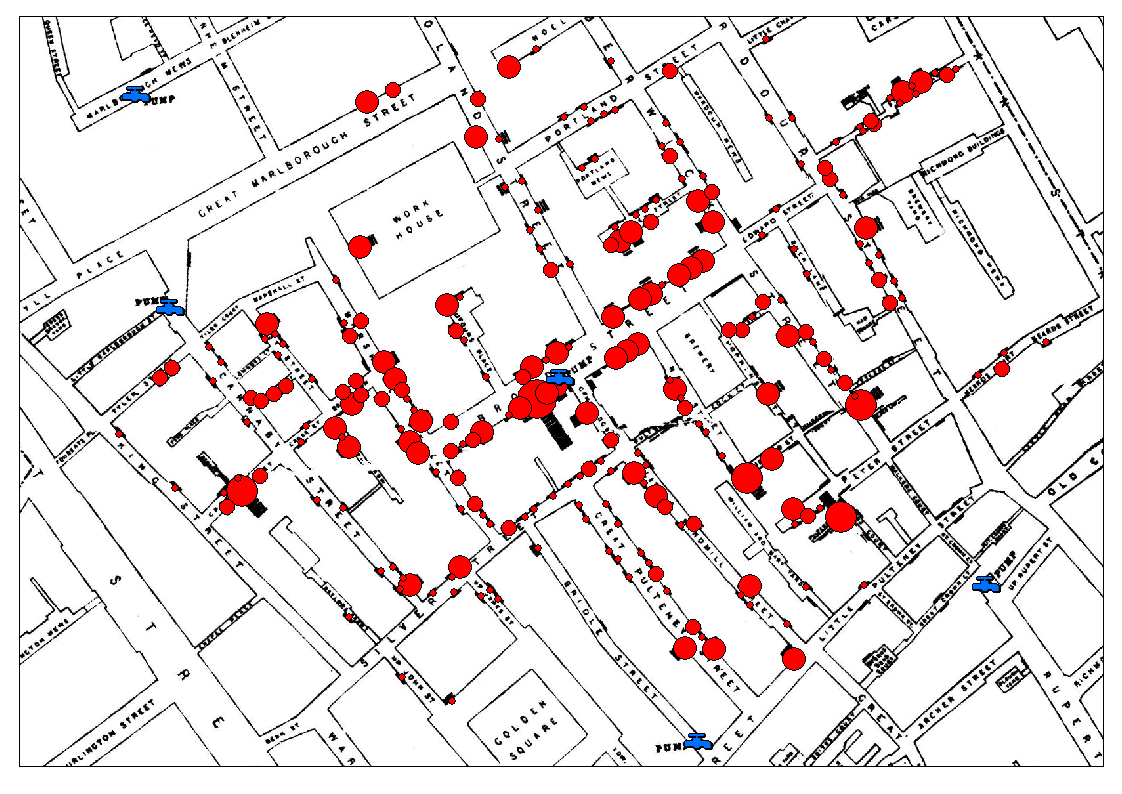
Mapa del cólera (John Snow, 1855)
Gráfico que muestra los casos de cólera durante la epidemia en Londres de 1854 y Las cruces la ubicación de las bombas de agua.
¿Por qué utilizar gráficos?¶
- El 70 % de los receptores sensoriales del cuerpo humano está dedicado a la visión.
Cerebro ha sido entrenado evolutivamente para interpretar la información visual de manera masiva.
“The eye and the visual cortex of the brain form a massively parallel processor that provides the highest bandwidth channel into human cognitive centers” — Colin Ware, Information Visualization, 2004.
Cuarteto de ANSCOMBE¶
El Cuarteto de Anscombe es un conjunto de cuatro conjuntos de datos que tienen las mismas estadísticas descriptivas (medias, varianzas, correlaciones y regresiones), pero que se ven muy diferentes cuando se visualizan. Fueron presentados por el estadístico Francis Anscombe en 1973 para demostrar la importancia de la visualización en el análisis de datos.
Los cuatro conjuntos de datos consisten en pares de variables x e y, y cada conjunto representa un tipo diferente de relación entre las variables. A simple vista, los cuatro conjuntos parecen tener distribuciones y relaciones completamente diferentes entre sí, pero cuando se analizan las estadísticas descriptivas, todas son idénticas.
from IPython.display import display_html
def display_side_by_side(*args):
html_str = ''
for df in args:
html_str += df.to_html()
html_str += ' '
display_html(
html_str.replace('table','table style="display:inline"'),
raw=True
)
import seaborn as sns
import matplotlib.pyplot as plt
# Cargar los datos del cuarteto de Anscombe
anscombe = sns.load_dataset("anscombe")
# Dividir los datos en cuatro conjuntos según el valor de "dataset"
ds1 = anscombe[anscombe['dataset'] == 'I']
ds2 = anscombe[anscombe['dataset'] == 'II']
ds3 = anscombe[anscombe['dataset'] == 'III']
ds4 = anscombe[anscombe['dataset'] == 'IV']
# Mostrar estadisticas para cada conjunto
x=" "
print(f"{10*x}Dataset I {13*x}Dataset II")
display_side_by_side(ds1.describe(),ds2.describe())
print()
print(f"{10*x}Dataset III {13*x}Dataset IV")
display_side_by_side(ds3.describe(),ds4.describe())
Dataset I Dataset II
| x | y | |
|---|---|---|
| count | 11.000000 | 11.000000 |
| mean | 9.000000 | 7.500909 |
| std | 3.316625 | 2.031568 |
| min | 4.000000 | 4.260000 |
| 25% | 6.500000 | 6.315000 |
| 50% | 9.000000 | 7.580000 |
| 75% | 11.500000 | 8.570000 |
| max | 14.000000 | 10.840000 |
| x | y | |
|---|---|---|
| count | 11.000000 | 11.000000 |
| mean | 9.000000 | 7.500909 |
| std | 3.316625 | 2.031657 |
| min | 4.000000 | 3.100000 |
| 25% | 6.500000 | 6.695000 |
| 50% | 9.000000 | 8.140000 |
| 75% | 11.500000 | 8.950000 |
| max | 14.000000 | 9.260000 |
Dataset III Dataset IV
| x | y | |
|---|---|---|
| count | 11.000000 | 11.000000 |
| mean | 9.000000 | 7.500000 |
| std | 3.316625 | 2.030424 |
| min | 4.000000 | 5.390000 |
| 25% | 6.500000 | 6.250000 |
| 50% | 9.000000 | 7.110000 |
| 75% | 11.500000 | 7.980000 |
| max | 14.000000 | 12.740000 |
| x | y | |
|---|---|---|
| count | 11.000000 | 11.000000 |
| mean | 9.000000 | 7.500909 |
| std | 3.316625 | 2.030579 |
| min | 8.000000 | 5.250000 |
| 25% | 8.000000 | 6.170000 |
| 50% | 8.000000 | 7.040000 |
| 75% | 8.000000 | 8.190000 |
| max | 19.000000 | 12.500000 |
# Mostrar correlaciones para cada conjunto
print(f"{5*x}Dataset I {10*x}Dataset II {10*x}Dataset III {10*x}Dataset IV")
display_side_by_side(ds1.corr(),ds2.corr(),ds3.corr(),ds4.corr())
Dataset I Dataset II Dataset III Dataset IV
| x | y | |
|---|---|---|
| x | 1.000000 | 0.816421 |
| y | 0.816421 | 1.000000 |
| x | y | |
|---|---|---|
| x | 1.000000 | 0.816237 |
| y | 0.816237 | 1.000000 |
| x | y | |
|---|---|---|
| x | 1.000000 | 0.816287 |
| y | 0.816287 | 1.000000 |
| x | y | |
|---|---|---|
| x | 1.000000 | 0.816521 |
| y | 0.816521 | 1.000000 |
# Crear una figura con cuatro subplots
fig, axs = plt.subplots(ncols=4, figsize=(16, 4))
# Graficar cada conjunto de datos en su respectivo subplot
sns.regplot(x='x', y='y', data=ds1, ax=axs[0], ci=None)
sns.regplot(x='x', y='y', data=ds2, ax=axs[1], ci=None)
sns.regplot(x='x', y='y', data=ds3, ax=axs[2], ci=None)
sns.regplot(x='x', y='y', data=ds4, ax=axs[3], ci=None)
# Agregar títulos a los subplots
axs[0].set_title('Dataset I')
axs[1].set_title('Dataset II')
axs[2].set_title('Dataset III')
axs[3].set_title('Dataset IV')
# Mostrar el gráfico
plt.show()
Paradoja de Simpson¶
La Paradoja de Simpson es un fenómeno en la visualización de datos que puede ocurrir cuando se analizan datos de diferentes subgrupos o categorías de una población. La paradoja se produce cuando una tendencia o patrón que aparece en cada subgrupo se invierte o desaparece cuando se combinan los datos de todos los subgrupos.
Supongamos que tienes datos de la tasa de éxito de un tratamiento médico para tres grupos de pacientes: uno con edad joven, uno con edad media y uno con edad avanzada. Los datos se presentan en la siguiente tabla:
| Grupo 1 | Grupo 2 | Grupo 3 | |
|---|---|---|---|
| Tasa de éxito | 90% | 85% | 70% |
| Número de casos | 100 | 200 | 300 |
En la tabla anterior, se puede observar que la tasa de éxito general del tratamiento es del 80%. Sin embargo, si se examina cada grupo de forma individual, la tasa de éxito para cada grupo es mayor en comparación con el promedio general. Esto es un ejemplo de la Paradoja de Simpson.
A continuación se presenta un código en Python que ilustra este ejemplo:
import pandas as pd
import matplotlib.pyplot as plt
# Crear un DataFrame con los datos
data = {'Grupo': ['Grupo 1', 'Grupo 2', 'Grupo 3'],
'Tasa de éxito': [0.9, 0.85, 0.7],
'Número de casos': [100, 200, 300]}
df = pd.DataFrame(data)
# Calcular la tasa de éxito general
general_success_rate = df['Tasa de éxito'].mean()
print('Tasa de éxito general:', general_success_rate)
# Graficar los datos
fig, ax = plt.subplots()
df.plot(x='Grupo', y='Tasa de éxito', kind='bar', ax=ax)
ax.axhline(y=general_success_rate, color='r', linestyle='--')
ax.set_ylabel('Tasa de éxito')
ax.set_title('Paradoja de Simpson')
plt.show()
Tasa de éxito general: 0.8166666666666668
Otro ejemplo sería aplicar un modelo de regresión líneal al conjunto de datos completos y luego aplicarlo al conjunto de datos separado por categorías.
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# Generate 'random' data
np.random.seed(0)
X = 2.5 * np.random.randn(100) + 1.5 # Array of 100 values with mean = 1.5, stddev = 2.5
res = 0.5 * np.random.randn(100) # Generate 100 residual terms
y = 2 + 0.3 * X + res # Actual values of Y
# Create pandas dataframe to store our X and y values
ds1 = pd.DataFrame({
'x': X+10,
'y': y+10}
).assign(label = 'Dataset I')
ds2 = pd.DataFrame({
'x': X,
'y': y}
).assign(label = 'Dataset II')
df = pd.concat([ds1,ds2])
print("Grafico para todo el conjunto de datos")
sns.lmplot (x='x', y='y', data=df, ci=None)
plt.show()
Grafico para todo el conjunto de datos
print("Grafico para los grupos por separados")
sns.lmplot (x='x', y='y', data=df, hue='label', ci=None)
plt.show()
Grafico para los grupos por separados
Teoría de visualización¶
La teoría de visualización se refiere a la investigación y el estudio de cómo las personas procesan, interpretan y comprenden información visual. La visualización puede involucrar cualquier tipo de información que pueda ser representada visualmente, incluyendo gráficos, diagramas, mapas, fotografías y videos.
La teoría de visualización tiene aplicaciones en una amplia variedad de campos, como la educación, la ciencia, la tecnología, el diseño y la comunicación. Algunos de los conceptos y principios importantes en la teoría de visualización incluyen:
- Percepción visual: Cómo procesamos y entendemos la información visual a través de nuestros sentidos.
- Cognición visual: Cómo procesamos y entendemos la información visual a través de nuestros procesos mentales, como la atención, la memoria y la toma de decisiones.
- Diseño visual: Cómo se pueden crear visualizaciones efectivas y atractivas para comunicar información de manera clara y efectiva.
- Interactividad visual: Cómo las visualizaciones interactivas pueden ayudar a los usuarios a explorar y comprender mejor la información visual.
Consejos generales¶
Noah Illinsky es un experto en visualización de datos y ha identificado cuatro pilares fundamentales de la visualización. Estos pilares son:
Contenido: El contenido se refiere a la información que se está visualizando. Para que la visualización sea efectiva, es importante tener una comprensión clara del contenido y cómo se relaciona con el objetivo de la visualización.
Función: La función se refiere al propósito de la visualización. ¿Qué se espera que haga la visualización? ¿Debe mostrar una tendencia, comparar datos o explorar patrones? Es importante tener en cuenta la función de la visualización para asegurarse de que se está diseñando de manera efectiva.
Forma: La forma se refiere a la apariencia visual de la visualización. Esto incluye cosas como el tipo de gráfico o diagrama utilizado, la paleta de colores y la tipografía. La forma debe ser coherente y legible para que la visualización sea fácil de entender.
Audiencia: La audiencia se refiere a las personas que verán la visualización. La comprensión de la audiencia es esencial para determinar el nivel de detalle y complejidad adecuados para la visualización. La visualización debe ser accesible y comprensible para su audiencia objetivo.
Elementos para la creación de una buena visualización¶
Claridad: La visualización debe ser clara y fácil de entender. Cualquier texto, etiqueta o leyenda debe ser fácil de leer, y los elementos gráficos deben estar dispuestos de manera lógica y fácil de seguir.
Integridad de los datos: Los datos que se utilizan para la visualización deben ser precisos y completos. Es importante que los datos sean confiables y estén bien documentados.
Contexto: La visualización debe proporcionar contexto para los datos que se muestran. Esto podría incluir información sobre la fuente de los datos, el período de tiempo que se está considerando o cualquier otra información relevante.
Diseño coherente: El diseño de la visualización debe ser coherente y cohesivo. Esto significa que los elementos de la visualización deben estar dispuestos de manera lógica y coherente, y que cualquier texto o etiqueta debe seguir un estilo visual consistente.
Interactividad: Si es posible, es útil incluir interactividad en la visualización. Esto puede permitir a los usuarios explorar y manipular los datos para obtener información más detallada.
Audiencia: La visualización debe estar diseñada con su audiencia en mente. Esto significa que el nivel de detalle y la complejidad de la visualización deben ser apropiados para la audiencia prevista.
Diseño estético: La visualización debe ser atractiva y bien diseñada. Esto no solo hace que la visualización sea más agradable de ver, sino que también puede ayudar a los usuarios a comprender mejor la información que se presenta.
Más Aspectos de la Visualización¶
Honestidad¶
El ojo humano no tiene la misma precisión al estimar distintas atribuciones:
- Largo: Bien estimado y sin sesgo, con un factor multiplicativo de 0.9 a 1.1.
- Área: Subestimado y con sesgo, con un factor multiplicativo de 0.6 a 0.9.
- Volumen: Muy subestimado y con sesgo, con un factor multiplicativo de 0.5 a 0.8.
Resulta inadecuado realizar gráficos de datos utilizando áreas o volúmenes si no queda claro la atribución utilizada.

Una pseudo-excepción la constituyen los pie-chart o gráficos circulares, porque el ojo humano distingue bien ángulos y segmentos de círculo, y porque es posible indicar los porcentajes respectivos.
# Pie chart, where the slices will be ordered and plotted counter-clockwise:
labels = 'Frogs', 'Hogs', 'Dogs', 'Logs'
sizes = [15, 30, 45, 10]
explode = (0, 0.1, 0, 0) # only "explode" the 2nd slice (i.e. 'Hogs')
fig1, ax1 = plt.subplots(figsize=(8, 8))
ax1.pie(
sizes,
explode=explode,
labels=labels,
autopct='%1.1f%%',
shadow=True,
startangle=90
)
ax1.axis('equal') # Equal aspect ratio ensures that pie is drawn as a circle.
plt.show()
Priorización¶
Dato más importante debe utilizar elemento de mejor percepción.
np.random.seed(42)
N = 31
x = np.arange(N)
y1 = 80 + 20 *x / N + 5 * np.random.rand(N)
y2 = 75 + 25 *x / N + 5 * np.random.rand(N)
fig, axs = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(16,8))
axs[0][0].plot(x, y1, 'ok')
axs[0][0].plot(x, y2, 'sk')
axs[0][1].plot(x, y1, 'ob')
axs[0][1].plot(x, y2, 'or')
axs[1][0].plot(x, y1, 'ob')
axs[1][0].plot(x, y2, '*k')
axs[1][1].plot(x, y1, 'sr')
axs[1][1].plot(x, y2, 'ob')
plt.show()
Percepción¶
No todos los elementos tienen la misma percepción a nivel del sistema visual. En particular, el color y la forma son elementos preatentivos: un color distinto o una forma distinta se reconocen de manera no conciente.
Ejemplos de elementos preatentivos.


El sistema visual humano puede estimar con precisión siguientes atributos visuales:
- Posición
- Largo
- Pendiente
- Ángulo
- Área
- Volumen
- Color
Utilice el atributo que se estima con mayor precisión cuando sea posible.
Colormaps¶
Puesto que la percepción del color tiene muy baja precisión, resulta inadecuado tratar de representar un valor numérico con colores.
- ¿Qué diferencia numérica existe entre el verde y el rojo?
- ¿Que asociación preexistente posee el color rojo, el amarillo y el verde?
- ¿Con cuánta precisión podemos distinguir valores en una escala de grises?

Python Landscape¶
Para empezar, PyViz es un sitio web que se dedica a ayudar a los usuarios a decidir dentro de las mejores herramientas de visualización open-source implementadas en Python, dependiendo de sus necesidades y objetivos. Mucho de lo que se menciona en esta sección está en detalle en la página web del proyecto PyViz.
Algunas de las librerías de visualización de Python más conocidas son:
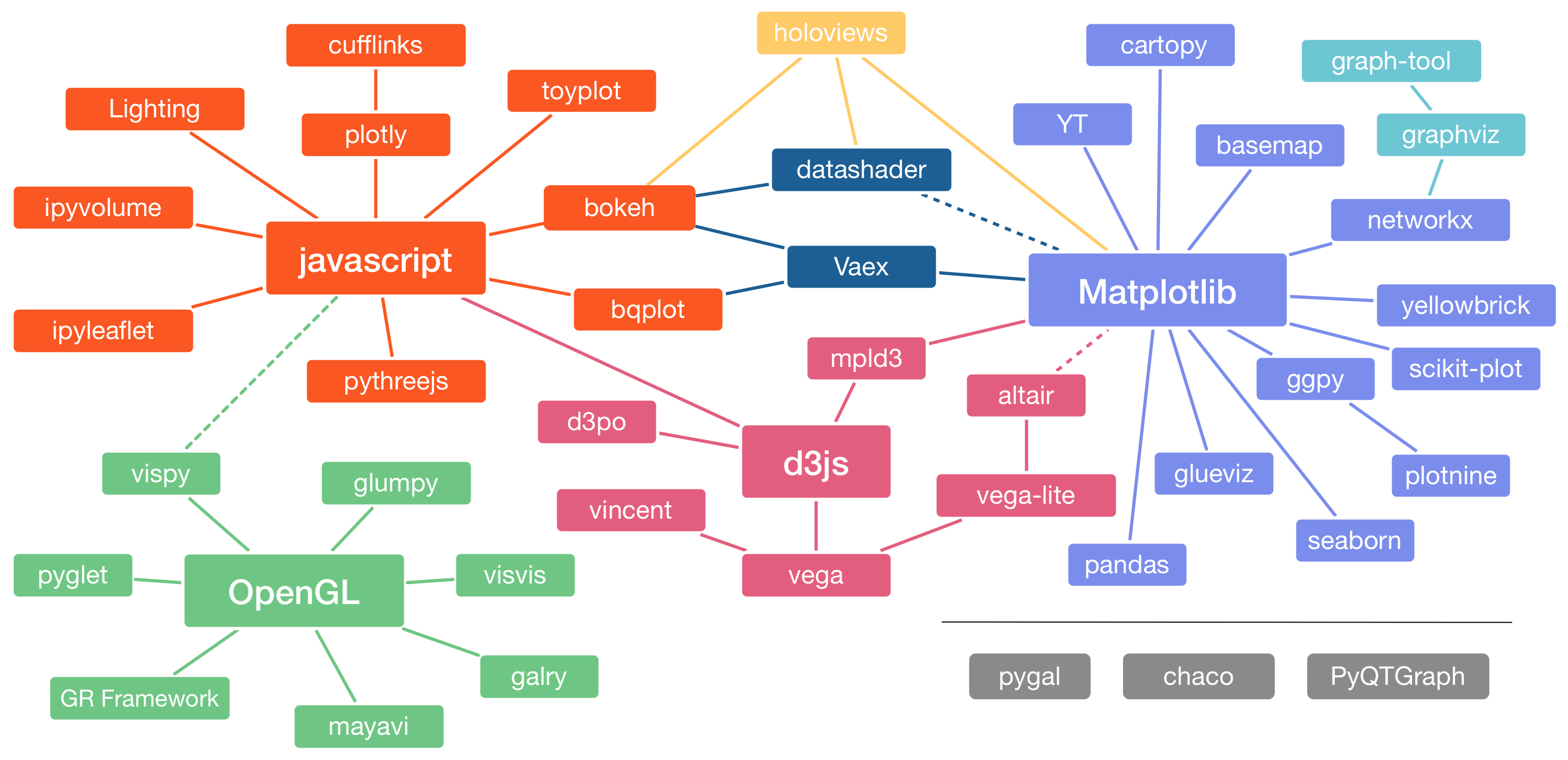
Este esquema es una adaptación de uno presentado en la charla The Python Visualization Landscape realizada por Jake VanderPlas en la PyCon 2017.
Cada una de estas librerías fue creada para satisfacer diferentes necesidades, algunas han ganado más adeptos que otras por uno u otro motivo. Tal como avanza la tecnología, estas librerías se actualizan o se crean nuevas, la importancia no recae en ser un experto en una, si no en saber adaptarse a las situaciones, tomar la mejor decicisión y escoger según nuestras necesidades y preferencias. Por ejemplo, matplotlib nació como una solución para imitar los gráficos de MATLAB (puedes ver la historia completa aquí), manteniendo una sintaxis similar y con ello poder crear gráficos estáticos de muy buen nivel.
Debido al éxito de matplotlib en la comunidad, nacen librerías basadas ella. Algunos ejemplos son:
seabornse basa enmatpĺotlibpero su nicho corresponde a las visualizaciones estadísticas.ggpyuna suerte de copia aggplot2perteneciente al lenguaje de programaciónR.networkxvisualizaciones de grafos.pandasno es una librería de visualización propiamente tal, pero utiliza amatplotplibcomo bakcned en los métodos con tal de crear gráficos de manera muy rápida, e.g.pandas.DataFrame.plot.bar()
Por otro lado, con tal de crear visualizaciones interactivas aparecen librerías basadas en javascript, algunas de las más conocidas en Python son:
bokehtiene como objetivo proporcionar gráficos versátiles, elegantes e incluso interactivos, teniendo una gran performance con grandes datasets o incluso streaming de datos.plotlyvisualizaciones interactivas que en conjunto aDash(de la misma empresa) permite crear aplicaciones webs, similar ashinydeR.D3.jsa pesar de estar basado enjavascriptse ha ganado un lugar en el corazón de toda la comunidad, debido a la ilimitada cantidad de visualizaciones que son posibles de hacer, por ejemplo, la malla interactiva que hizo un estudiante de la UTFSM está hecha enD3.js.
De las librerías más recientes está Altair, que consiste en visualizaciones declarativas (ya lo veremos en el próximo laboratorio). Construída sobre Vega-Lite, a su vez que esté está sobre Vega y este finalmente sobre D3.js. Altair permite crear visualizaciones estáticas e interactivas con pocas líneas de código, sin embargo, al ser relativamente nueva, aún existen funcionalidades en desarrollo o que simplemente aún no existen en esta librería pero en otras si.