Conceptos Básicos ML¶
Machine Learning (ML) es una rama de la inteligencia artificial que permite a las computadoras aprender de datos y hacer predicciones sin programación explícita. A través de algoritmos, las máquinas identifican patrones y toman decisiones, transformando industrias y mejorando la eficiencia. En esta sección, exploraremos los conceptos fundamentales de ML.
🎯 Objetivos:
- Entender conceptos básicos de ML
- Entender el proceso de aprendizaje supervisado (regresión y clasificación)
- Heramientas útiles de Scikit-Learn
Cómo Usar Scikit-Learn¶
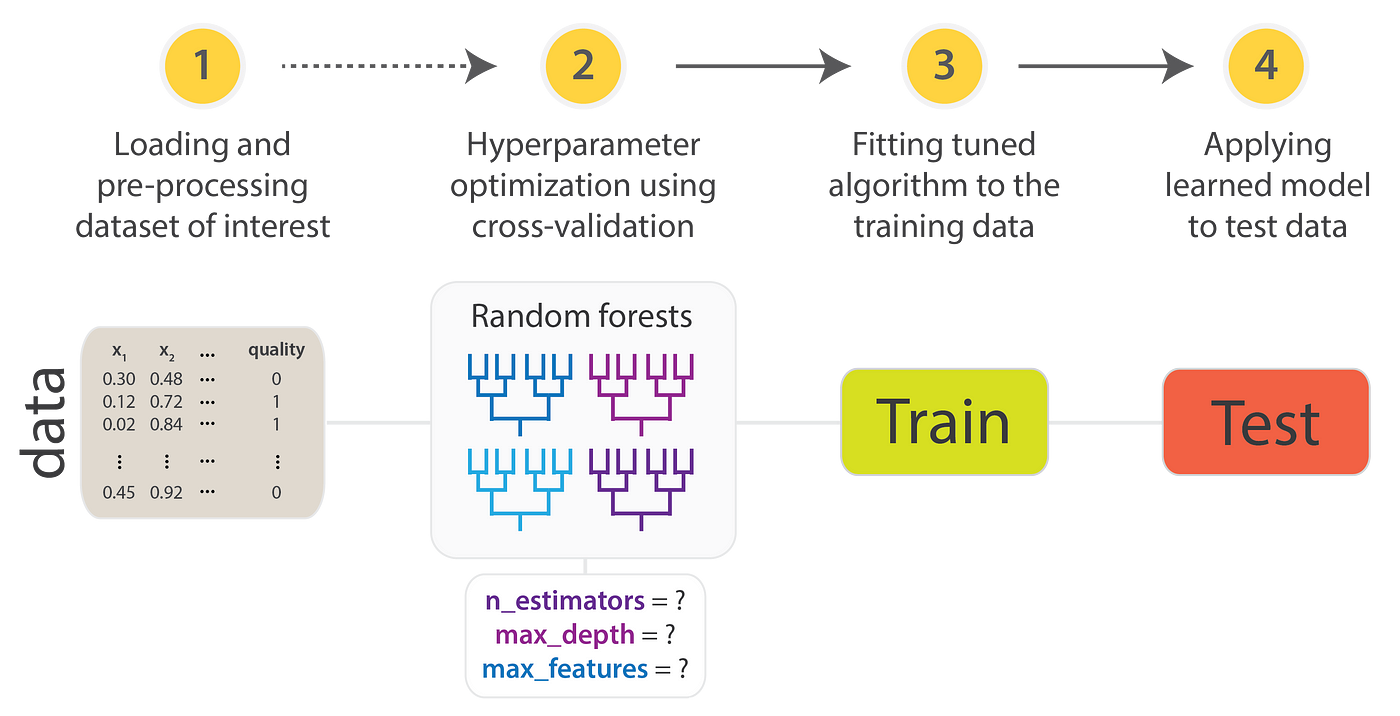
Para utilizar la API de Scikit-Learn, sigue estos pasos:
- Organizar los datos: Estructura tus datos en una matriz de características ($X$) y un vector de objetivos ($y$).
- Seleccionar un modelo: Importa la clase de estimador adecuada desde Scikit-Learn.
- Definir hiperparámetros: Instancia la clase del modelo con los hiperparámetros deseados.
- Ajustar el modelo: Usa el método
fit()con los datos para entrenar el modelo. - Aplicar el modelo a nuevos datos:
- Para aprendizaje supervisado, utiliza
predict()para generar predicciones. - Para aprendizaje no supervisado, emplea
transform()opredict()para inferir propiedades o transformar los datos.
- Para aprendizaje supervisado, utiliza
Analisis Supervisado: Clasificación¶
Un ejemplo clásico es el conjunto de datos Iris, analizado por Ronald Fisher en 1936, que utiliza esta estructura para presentar las características de diferentes especies de flores.
Descripción de las Columnas
- sepal_length: Longitud del sépalo en centímetros.
- sepal_width: Ancho del sépalo en centímetros.
- petal_length: Longitud del pétalo en centímetros.
- petal_width: Ancho del pétalo en centímetros.
- species: Especie de la flor (setosa, versicolor, virginica).
# Carga el conjunto de dato
import seaborn as sns
iris = sns.load_dataset('iris')
iris.head()
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
En este conjunto de datos, cada fila representa una flor observada, y el total de filas indica cuántas flores hay en el conjunto, conocido como n_samples. A estas filas se les denomina muestras (samples).
Por otro lado, cada columna contiene información específica sobre cada muestra, denominada característica (feature). El total de columnas se refiere como n_features.
Matriz de características y Arreglo de Etiquetas¶
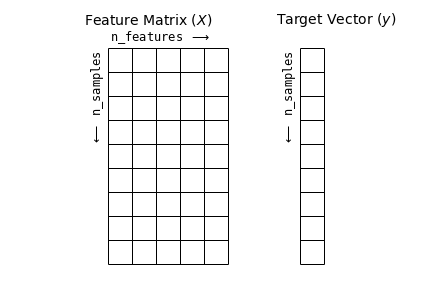
La matriz de características es la representación de los datos de entrada en un problema de aprendizaje automático. Se trata de una matriz bidimensional con forma [n_samples, n_features], donde las filas representan muestras y las columnas las características o atributos que describen cada muestra.
Las características suelen ser valores cuantitativos, aunque pueden ser booleanos o discretos. Por convención, esta matriz se almacena en una variable llamada X.
# Matriz de características
X = iris.drop('species',axis=1)
X
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 |
| ... | ... | ... | ... | ... |
| 145 | 6.7 | 3.0 | 5.2 | 2.3 |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 |
150 rows × 4 columns
Arreglo de Etiquetas¶
Además de la matriz de características X, trabajamos con un arreglo de etiquetas (target array), comúnmente llamado y. Este arreglo es unidimensional y tiene una longitud igual a n_samples, almacenando los valores objetivo para cada muestra. Los valores pueden ser numéricos continuos o clases discretas.
Aunque algunos estimadores de Scikit-Learn permiten una matriz bidimensional [n_samples, n_targets], generalmente nos enfocamos en el caso más común de un arreglo unidimensional.
# target
y = iris['species']
y
0 setosa
1 setosa
2 setosa
3 setosa
4 setosa
...
145 virginica
146 virginica
147 virginica
148 virginica
149 virginica
Name: species, Length: 150, dtype: object
Conjunto de Entrenamiento y Prueba¶
En el aprendizaje automático, el conjunto de entrenamiento (train set) y el conjunto de prueba (test set) son dos subconjuntos de datos fundamentales.
El conjunto de entrenamiento se utiliza para entrenar el modelo, mientras que el conjunto de prueba se reserva para evaluar su rendimiento y capacidad de generalización a datos no vistos.
El conjunto de entrenamiento es un subconjunto de datos utilizado para ajustar los parámetros del modelo y aprender la relación entre las variables de entrada y la salida. En esencia, sirve para entrenar al modelo.
El conjunto de prueba es otro subconjunto, separado del proceso de entrenamiento, empleado para evaluar el rendimiento del modelo. Permite medir su capacidad de generalización al enfrentarlo a datos nuevos y no vistos previamente.
La función train_test_split de Scikit-learn es una herramienta clave para dividir un conjunto de datos en subconjuntos de entrenamiento y prueba. Esta función permite especificar la proporción de datos que se asignará a cada conjunto, siendo el valor predeterminado 75% para entrenamiento y 25% para prueba. Además, acepta tanto los datos como sus etiquetas correspondientes como entradas.
A continuación, se muestra un ejemplo de cómo utilizarla:
from sklearn.model_selection import train_test_split
# separar informacion
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.25, random_state=42)
print(f"dimensiones de X_train: {X_train.shape}")
print(f"dimensiones de y_train: {y_train.shape}")
print("")
print(f"dimensiones de X_test: {X_test.shape}")
print(f"dimensiones de y_test: {y_test.shape}")
dimensiones de X_train: (112, 4) dimensiones de y_train: (112,) dimensiones de X_test: (38, 4) dimensiones de y_test: (38,)
La función train_test_split(X, y, test_size=0.25, random_state=42) divide los datos en un conjunto de entrenamiento y otro de prueba.
Xson los datos de entrada yylas etiquetas.test_size=0.25asigna el 25% de los datos al conjunto de prueba y el 75% al de entrenamiento.random_state=42asegura que la división sea reproducible, generando los mismos subconjuntos cada vez que se ejecuta el código.
Reglas de Separación
Es esencial dividir los datos en conjuntos de entrenamiento y prueba para entrenar el modelo y evaluar su rendimiento en datos no vistos. Generalmente, el conjunto de entrenamiento ocupa entre el 70% y el 80%, mientras que el de prueba entre el 20% y el 30%. En conjuntos grandes, se puede asignar más al entrenamiento.
Referencia de división:
| Número de filas | Entrenamiento | Prueba |
|---|---|---|
| 100 - 1,000 | 70% | 30% |
| 1,000 - 100,000 | 80% | 20% |
| Más de 100,000 | 90% | 10% |
Selección de una Clase de Modelo¶
En Scikit-Learn, cada modelo de aprendizaje automático se representa como una clase de Python. Por ejemplo, para predecir la especie de flores en el conjunto de datos Iris, podemos utilizar una clase de clasificación, como la regresión logística. Este enfoque simplifica la construcción y evaluación del modelo, permitiendo clasificar las flores en función de sus características, como la longitud y el ancho de los sépalos y pétalos.
Nota: Existen diversos modelos para tareas de clasificación. Puedes consultar la lista completa en el siguiente enlace.
from sklearn.linear_model import LogisticRegression
# Crear el modelo de regresión logística
model = LogisticRegression()
# Entrenar el modelo con el conjunto de entrenamiento
model.fit(X_train, y_train)
LogisticRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LogisticRegression()
Es fundamental destacar que al crear una instancia de un modelo en Scikit-Learn, la única acción realizada es almacenar los valores de los hiperparámetros. En este momento, aún no hemos aplicado el modelo a ningún dato. La API de Scikit-Learn establece una clara distinción entre la selección del modelo y su aplicación a los datos.
Los hiperparámetros son configuraciones que se establecen antes de entrenar el modelo y pueden influir significativamente en su rendimiento. Estos parámetros controlan aspectos como la complejidad del modelo, el tamaño del árbol en un árbol de decisión, la tasa de aprendizaje en un modelo de gradiente, o el número de vecinos en un clasificador KNN. La elección adecuada de los hiperparámetros puede mejorar la precisión del modelo y ayudar a evitar el sobreajuste.
Ejemplo con el modelo de regresión logística
model = LogisticRegression(solver='liblinear', C=0.5, max_iter=200)
model.fit(X_train, y_train)
Predicción¶
En el ámbito del aprendizaje automático, la predicción se refiere al proceso mediante el cual un modelo utiliza datos de entrada para estimar resultados o clasificaciones. A continuación, se muestra cómo se puede realizar una predicción utilizando un modelo de regresión logística en el conjunto de datos Iris.
# Realizar predicciones sobre el conjunto de prueba
y_pred = model.predict(X_test)
# Mostrar las predicciones
print("Predicciones:", y_pred)
Predicciones: ['versicolor' 'setosa' 'virginica' 'versicolor' 'versicolor' 'setosa' 'versicolor' 'virginica' 'versicolor' 'versicolor' 'virginica' 'setosa' 'setosa' 'setosa' 'setosa' 'versicolor' 'virginica' 'versicolor' 'versicolor' 'virginica' 'setosa' 'virginica' 'setosa' 'virginica' 'virginica' 'virginica' 'virginica' 'virginica' 'setosa' 'setosa' 'setosa' 'setosa' 'versicolor' 'setosa' 'setosa' 'virginica' 'versicolor' 'setosa']
Métricas¶
La efectividad de estas predicciones es crucial y se evalúa a través de diversas métricas que cuantifican el rendimiento del modelo. Estas métricas permiten analizar cómo de bien el modelo ha aprendido a partir de los datos de entrenamiento y su capacidad para generalizar a nuevos datos.
En esta sección, exploraremos la importancia de la matriz de confusión y las métricas de evaluación, que nos ayudarán a entender y optimizar el rendimiento de nuestros modelos de clasificación.
Matriz de Confusión¶
La matriz de confusión es una herramienta esencial para evaluar el rendimiento de un modelo de clasificación. Proporciona una representación visual que resume las predicciones realizadas por el modelo y las compara con los valores reales.
Para la clasificación binaria (por ejemplo, clases 0 y 1), la matriz de confusión tiene la siguiente estructura:
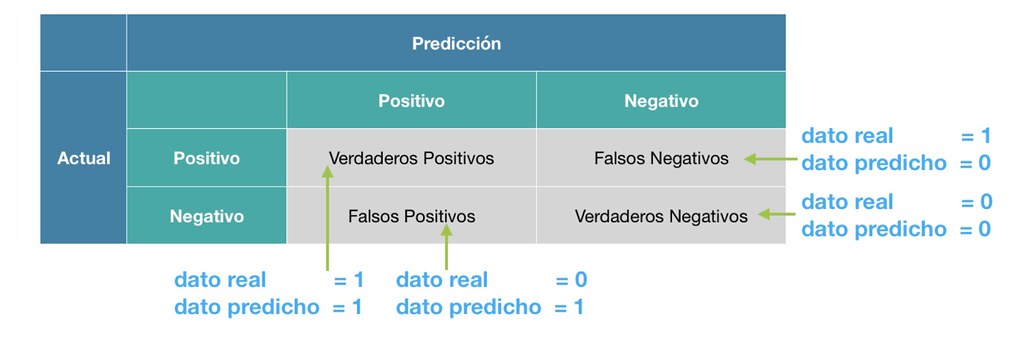
En esta matriz, se definen los siguientes componentes:
- TP (Verdadero Positivo): El modelo predijo correctamente la clase positiva.
- FP (Falso Positivo): El modelo predijo incorrectamente la clase positiva cuando realmente era negativa.
- FN (Falso Negativo): El modelo predijo incorrectamente la clase negativa cuando realmente era positiva.
- TN (Verdadero Negativo): El modelo predijo correctamente la clase negativa.
En resumen, TP y TN representan las predicciones correctas del modelo, mientras que FP y FN indican los errores de clasificación.
La siguiente imagen ilustra los conceptos de FN y FP:

Ahora, vamos a calcular la matriz de confusión utilizando el comando confusion_matrix de Scikit-Learn:
from sklearn.metrics import confusion_matrix
# Realizar predicciones sobre el conjunto de prueba
y_pred = model.predict(X_test)
# Calcular la matriz de confusión
cm = confusion_matrix(y_test, y_pred)
# Mostrar la matriz de confusión
print("Matriz de Confusión:")
print(cm)
Matriz de Confusión: [[15 0 0] [ 0 11 0] [ 0 0 12]]
Métricas de Evaluación¶
En el contexto de clasificación, el objetivo es maximizar la cantidad de TP (Verdaderos Positivos) y TN (Verdaderos Negativos), mientras se minimizan los FP (Falsos Positivos) y FN (Falsos Negativos). Para evaluar el rendimiento del modelo, se utilizan las siguientes métricas:
Accuracy (Precisión Global):
- Mide la proporción de predicciones correctas (positivas y negativas) sobre el total de casos.
$$ accuracy(y, \hat{y}) = \frac{TP + TN}{TP + TN + FP + FN} $$
Recall (Sensibilidad o Tasa de Verdaderos Positivos):
- Evalúa la capacidad del modelo para identificar correctamente las muestras positivas.
$$ recall(y, \hat{y}) = \frac{TP}{TP + FN} $$
Precision (Precisión Positiva):
- Indica la proporción de verdaderos positivos sobre todas las predicciones positivas.
$$ precision(y, \hat{y}) = \frac{TP}{TP + FP} $$
F-score (F1-Score):
- Es la media armónica de la precisión y el recall, proporcionando un balance entre ambos.
$$ fscore(y, \hat{y}) = 2 \times \frac{precision(y, \hat{y}) \times recall(y, \hat{y})}{precision(y, \hat{y}) + recall(y, \hat{y})} $$
Veamos un ejemplo práctico donde calculamos estas métricas utilizando sklearn.metrics:
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score, confusion_matrix
# Calcular las métricas
accuracy = accuracy_score(y_test, y_pred)
recall = recall_score(y_test, y_pred, average='weighted')
precision = precision_score(y_test, y_pred, average='weighted')
f1 = f1_score(y_test, y_pred, average='weighted')
# Mostrar los resultados
print(f'Accuracy (Precisión Global): {accuracy:.2f}')
print(f'Recall (Sensibilidad): {recall:.2f}')
print(f'Precision (Precisión Positiva): {precision:.2f}')
print(f'F1-Score: {f1:.2f}')
Accuracy (Precisión Global): 1.00 Recall (Sensibilidad): 1.00 Precision (Precisión Positiva): 1.00 F1-Score: 1.00
Resultados:
- Accuracy: 1.00: El 100% de las predicciones fueron correctas, lo que indica que el modelo no cometió errores.
- Recall: 1.00: El modelo identificó el 100% de las muestras positivas correctamente, sin pasar por alto ninguna.
- Precision: 1.00: El 100% de las predicciones positivas fueron realmente positivas, lo que significa que no hubo falsos positivos.
- F1-Score: 1.00: Este valor perfecto indica un balance ideal entre precisión y recall, reflejando un modelo excepcional en la identificación correcta de las clases.
Nota: Se utiliza
average='weighted'cuando se tienen tres o más clases en un conjunto de datos. Esto permite calcular las métricas como precisión, recall y F1-Score tomando en cuenta la proporción de cada clase. Por ejemplo, si una clase es más frecuente que otra, su contribución al resultado final será mayor. Si solo hay dos clases, este argumento se ignora, ya que las métricas se calculan directamente sin necesidad de ponderar.
Analisis Supervisado: Regresión¶
Un ejemplo clásico es el conjunto de datos California Housing, que se utiliza para predecir el valor mediano de las viviendas en California en base a diversas características. Este conjunto de datos es ampliamente utilizado en la práctica de modelos de regresión.
Descripción de las Columnas
- MedInc: Ingreso mediano de los hogares en la unidad de censos (en miles de dólares).
- HouseAge: Edad mediana de las casas en la unidad de censos (en años).
- AveRooms: Número promedio de habitaciones por vivienda.
- AveOccup: Promedio de ocupantes por vivienda.
- Latitude: Latitud de la ubicación de la vivienda.
- Longitude: Longitud de la ubicación de la vivienda.
- Population: Número de personas que viven en la unidad de censos.
- Households: Número de hogares en la unidad de censos.
Teniendo en cuenta lo anterior, el proceso hasta el momento de entrenar el modelo es similar al de un problema de clasificación. Sin embargo, es importante reconocer que, en el caso de la regresión, debemos enfocarnos en entender las métricas específicas que la evalúan. A continuación, explicaremos estas métricas asociadas a la regresión.
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# Cargar el conjunto de datos de California Housing
data = fetch_california_housing()
california = pd.DataFrame(data.data, columns=data.feature_names)
california['price'] = data.target
california.head()
| MedInc | HouseAge | AveRooms | AveBedrms | Population | AveOccup | Latitude | Longitude | price | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 8.3252 | 41.0 | 6.984127 | 1.023810 | 322.0 | 2.555556 | 37.88 | -122.23 | 4.526 |
| 1 | 8.3014 | 21.0 | 6.238137 | 0.971880 | 2401.0 | 2.109842 | 37.86 | -122.22 | 3.585 |
| 2 | 7.2574 | 52.0 | 8.288136 | 1.073446 | 496.0 | 2.802260 | 37.85 | -122.24 | 3.521 |
| 3 | 5.6431 | 52.0 | 5.817352 | 1.073059 | 558.0 | 2.547945 | 37.85 | -122.25 | 3.413 |
| 4 | 3.8462 | 52.0 | 6.281853 | 1.081081 | 565.0 | 2.181467 | 37.85 | -122.25 | 3.422 |
# Características dy Target
X = california.drop(columns=['price'])
y = california['price']
# Dividir el conjunto de datos en entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Crear el modelo de regresión lineal
model = LinearRegression()
# Entrenar el modelo con el conjunto de entrenamiento
model.fit(X_train, y_train)
# Realizar predicciones sobre el conjunto de prueba
y_pred = model.predict(X_test)
# Imprimir las predicciones
print(y_pred)
[0.71912284 1.76401657 2.70965883 ... 4.46877017 1.18751119 2.00940251]
Métricas¶
La efectividad de las predicciones en problemas de regresión es fundamental y se evalúa mediante diversas métricas que cuantifican el rendimiento del modelo. Estas métricas permiten analizar qué tan bien el modelo ha aprendido de los datos de entrenamiento y su capacidad para generalizar a nuevos datos.
Métricas de Evaluación¶
El resultado de las predicciones nos proporciona el error de estimación para cada muestra (o fila). Para resumir este error, empleamos métricas de evaluación, que se dividen en dos categorías principales:
Métricas Absolutas: Estas métricas miden el error sin escalar los valores. Las métricas absolutas más comunes son:
- Mean Absolute Error (MAE): Esta métrica calcula el promedio de los errores absolutos entre las predicciones y los valores reales, proporcionando una medida clara del error promedio.
$$ \textrm{MAE}(y,\hat{y}) = \dfrac{1}{n}\sum_{t=1}^{n}\left | y_{t}-\hat{y}_{t}\right | $$
- Root Mean Squared Error (RMSE): RMSE mide la raíz cuadrada del promedio de los errores al cuadrado. Esta métrica penaliza más fuertemente los errores grandes, lo cual es útil en contextos donde los errores significativos son especialmente indeseables.
$$ \textrm{RMSE}(y,\hat{y}) = \left( \dfrac{1}{n}\sum_{t=1}^{n}\left ( y_{t}-\hat{y}_{t}\right )^2 \right)^{1/2} $$
Métricas Porcentuales: Estas métricas evalúan el error de manera escalada, acotando los resultados entre 0 y 1, donde 0 indica un ajuste perfecto y 1 refleja un mal ajuste. Es importante destacar que, en algunos casos, estas métricas pueden superar el valor de 1.
- Mean Absolute Percentage Error (MAPE): MAPE calcula el error absoluto como un porcentaje del valor real, ofreciendo una forma de entender el error en términos relativos. $$ \textrm{MAPE}(y,\hat{y}) = \dfrac{1}{n}\sum_{t=1}^{n}\left | \frac{y_{t}-\hat{y}_{t}}{y_{t}} \right | $$
Veamos un ejemplo práctico donde obtendremos estas métricas utilizando sklearn.metrics:
from sklearn.metrics import mean_absolute_error, root_mean_squared_error, mean_absolute_percentage_error
# Realizar predicciones sobre el conjunto de prueba
y_pred = model.predict(X_test)
# Calcular las métricas de evaluación
mae = mean_absolute_error(y_test, y_pred)
rmse = root_mean_squared_error(y_test, y_pred) # RMSE
mape = mean_absolute_percentage_error(y_test, y_pred)
# Mostrar los resultados
print(f'Error Absoluto Medio (MAE): {mae:.2f}')
print(f'Raíz del Error Cuadrático Medio (RMSE): {rmse:.2f}')
print(f'Error Porcentual Absoluto Medio (MAPE): {mape:.2f}')
Error Absoluto Medio (MAE): 0.53 Raíz del Error Cuadrático Medio (RMSE): 0.75 Error Porcentual Absoluto Medio (MAPE): 0.32
Resultados:
- Error Absoluto Medio (MAE): 0.53: Indica que, en promedio, las predicciones se desvían en 0.53 unidades de los valores reales.
- Raíz del Error Cuadrático Medio (RMSE): 0.75: Mide que la desviación típica de las predicciones es de aproximadamente 0.75 unidades.
- Error Porcentual Absoluto Medio (MAPE): 0.32: Significa que, en promedio, las predicciones se desvían un 32% respecto a los valores reales.
Otros Conceptos Importantes¶
Normalizar y estandarizar los datos¶
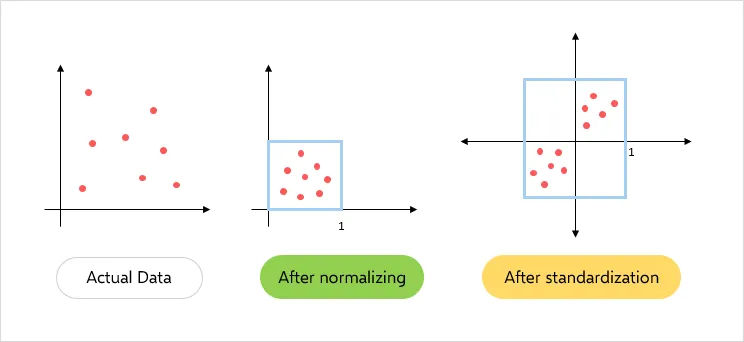
La normalización y la estandarización son técnicas clave en el preprocesamiento de datos que ayudan a mejorar el rendimiento de los modelos de aprendizaje automático.
Normalización:
- La normalización es el proceso de escalar los datos para que se encuentren dentro de un rango específico, generalmente entre 0 y 1. Esto se logra utilizando la siguiente fórmula: $$ X' = \frac{X - X_{\text{min}}}{X_{\text{max}} - X_{\text{min}}} $$
- La normalización es útil cuando las características tienen diferentes escalas y se desea que todas tengan el mismo peso en el modelo.
Estandarización:
- La estandarización transforma los datos para que tengan una media de 0 y una desviación estándar de 1. Se utiliza la siguiente fórmula: $$ Z = \frac{X - \mu}{\sigma} $$ donde $ \mu $ es la media y $ \sigma $ es la desviación estándar.
- La estandarización es especialmente útil para algoritmos que asumen que los datos están distribuidos normalmente, como la regresión logística y las máquinas de soporte vectorial.
Ambas técnicas son importantes para asegurar que los modelos de aprendizaje automático funcionen correctamente y mejoren su capacidad de generalización.
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler, StandardScaler
# Cargar el conjunto de datos Iris
iris = load_iris()
X = pd.DataFrame(iris.data, columns=iris.feature_names)
# Mostrar los datos originales
print("Datos originales:")
X.head()
Datos originales:
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 |
# Normalización
normalizer = MinMaxScaler()
X_normalized = normalizer.fit_transform(X)
# Convertir el resultado de la normalización a un DataFrame
X_normalized = pd.DataFrame(X_normalized, columns=X.columns)
# Mostrar los datos normalizados
print("\nDatos normalizados:")
X_normalized.head()
Datos normalizados:
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | 0.222222 | 0.625000 | 0.067797 | 0.041667 |
| 1 | 0.166667 | 0.416667 | 0.067797 | 0.041667 |
| 2 | 0.111111 | 0.500000 | 0.050847 | 0.041667 |
| 3 | 0.083333 | 0.458333 | 0.084746 | 0.041667 |
| 4 | 0.194444 | 0.666667 | 0.067797 | 0.041667 |
# Estandarización
scaler = StandardScaler()
X_standardized = scaler.fit_transform(X)
# Convertir el resultado de la estandarización a un DataFrame
X_standardized = pd.DataFrame(X_standardized, columns=X.columns)
# Mostrar los datos estandarizados
print("\nDatos estandarizados:")
X_standardized.head()
Datos estandarizados:
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | -0.900681 | 1.019004 | -1.340227 | -1.315444 |
| 1 | -1.143017 | -0.131979 | -1.340227 | -1.315444 |
| 2 | -1.385353 | 0.328414 | -1.397064 | -1.315444 |
| 3 | -1.506521 | 0.098217 | -1.283389 | -1.315444 |
| 4 | -1.021849 | 1.249201 | -1.340227 | -1.315444 |
One Hot Encoding¶

One Hot Encoding es una técnica utilizada en el preprocesamiento de datos para convertir variables categóricas en un formato que puede ser fácilmente utilizado por algoritmos de aprendizaje automático. Dado que muchos modelos de machine learning requieren entradas numéricas, esta técnica transforma cada categoría en una columna binaria (0 o 1), lo que permite representar la presencia o ausencia de una categoría específica.
Por ejemplo, si tenemos una variable categórica llamada "Color" con las categorías "Rojo", "Verde" y "Azul", One Hot Encoding convertirá esta variable en tres nuevas columnas: "Color_Rojo", "Color_Verde" y "Color_Azul". Si un registro tiene el color "Rojo", la columna "Color_Rojo" será 1 y las otras dos serán 0.
Esta transformación es esencial para evitar que los modelos interpreten incorrectamente la relación ordinal entre las categorías y ayuda a mejorar la precisión del modelo en la clasificación y regresión.
import pandas as pd
# Crear un DataFrame de ejemplo con una variable categórica
data = {
'Color': ['Rojo', 'Verde', 'Azul', 'Rojo', 'Verde'],
'Cantidad': [5, 3, 2, 8, 6]
}
df = pd.DataFrame(data)
# Mostrar el DataFrame original
print("DataFrame Original:")
df
DataFrame Original:
| Color | Cantidad | |
|---|---|---|
| 0 | Rojo | 5 |
| 1 | Verde | 3 |
| 2 | Azul | 2 |
| 3 | Rojo | 8 |
| 4 | Verde | 6 |
# Aplicar One Hot Encoding
df_encoded = pd.get_dummies(df, columns=['Color'], prefix='Color')
# Mostrar el DataFrame después de One Hot Encoding
print("\nDataFrame con One Hot Encoding:")
df_encoded
DataFrame con One Hot Encoding:
| Cantidad | Color_Azul | Color_Rojo | Color_Verde | |
|---|---|---|---|---|
| 0 | 5 | False | True | False |
| 1 | 3 | False | False | True |
| 2 | 2 | True | False | False |
| 3 | 8 | False | True | False |
| 4 | 6 | False | False | True |
Referencias¶
- Modelos de Regresión en Scikit-Learn: Documentación sobre los modelos de regresión disponibles en Scikit-Learn.
- Modelos de Clasificación en Scikit-Learn: Documentación sobre los modelos de clasificación disponibles en Scikit-Learn.
