Overfitting I¶

Introducción¶

Overfitting y Underfitting en Machine Learning

• Overfitting: Sucede cuando el modelo se ajusta demasiado a los datos de entrenamiento, capturando ruido y patrones específicos que no generalizan bien. Esto es común en modelos complejos y puede evitarse mediante validación cruzada para comparar rendimiento en datos de prueba.

• Underfitting: Ocurre cuando el modelo es demasiado simple y no capta patrones importantes, presentando bajo ajuste y alto sesgo.

Escogiendo el Mejor Modelo

La complejidad del modelo afecta el riesgo de sobreajuste. No hay una regla exacta, pero se pueden usar herramientas de validación para equilibrar ajuste y generalización.

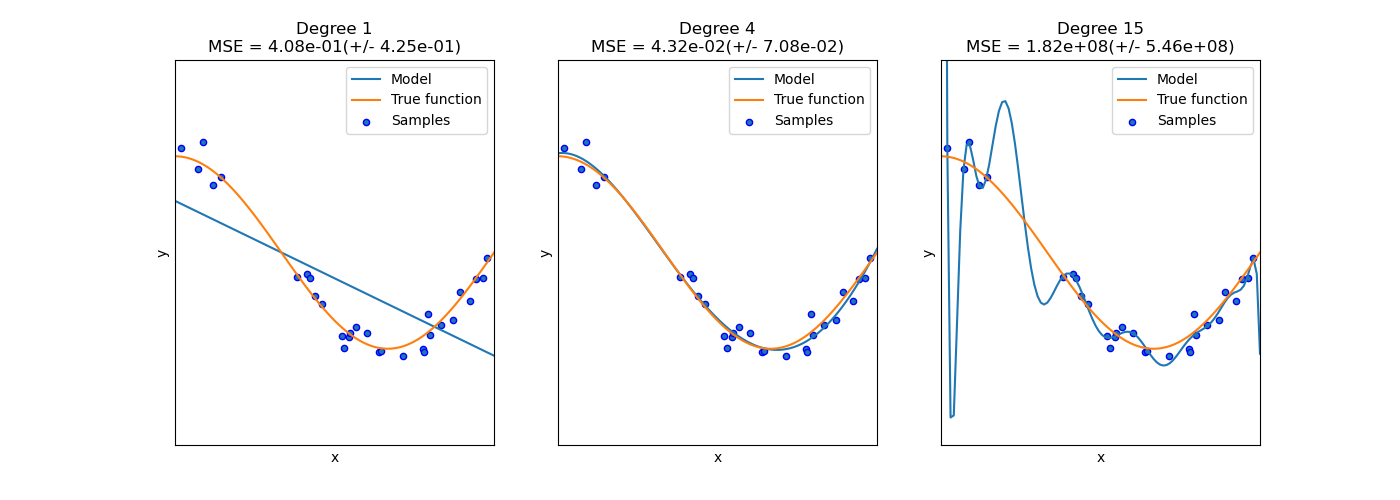
Ejemplo de Ajuste con Función Sinusoidal¶

Veamos un ejemplo simple en Python donde ajustaremos un modelo de Árbol de Decisión (DT) sobre una función sinusoidal.

In [14]:

# Librerías
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
import random

# Configuración de semilla y gráficos
random.seed(1982)
%matplotlib inline
sns.set_palette("deep", desat=0.6)
sns.set_context(rc={"figure.figsize": (12, 6)})

# Crear dataset sinusoidal con ruido
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(16))  # Añadir ruido

# Dividir los datos en entrenamiento y evaluación
x_train, x_eval, y_train, y_eval = train_test_split(X, y, test_size=0.35, random_state=1982)

# Definir modelos con distintos niveles de complejidad
regr_underfit = DecisionTreeRegressor(max_depth=1)   # Underfitting
regr_overfit = DecisionTreeRegressor(max_depth=10)   # Overfitting

# Entrenar los modelos
regr_underfit.fit(x_train, y_train)
regr_overfit.fit(x_train, y_train)

# Generar predicciones
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_underfit = regr_underfit.predict(X_test)
y_overfit = regr_overfit.predict(X_test)

# Visualización de resultados
fig, ax = plt.subplots(figsize=(12, 6))
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="Datos")
plt.plot(X_test, y_underfit, color="red", linestyle="--", label="Underfitting (max_depth=1)", linewidth=2)
plt.plot(X_test, y_overfit, color="green", linestyle=":", label="Overfitting (max_depth=10)", linewidth=2)

# Etiquetas y leyenda
plt.xlabel("Datos")
plt.ylabel("Objetivo")
plt.title("Ajuste de Árbol de Decisión en Datos Sinusoidales")
plt.legend()
plt.show()

# Librerías import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns from sklearn.model_selection import train_test_split from sklearn.tree import DecisionTreeRegressor import random # Configuración de semilla y gráficos random.seed(1982) %matplotlib inline sns.set_palette("deep", desat=0.6) sns.set_context(rc={"figure.figsize": (12, 6)}) # Crear dataset sinusoidal con ruido rng = np.random.RandomState(1) X = np.sort(5 * rng.rand(80, 1), axis=0) y = np.sin(X).ravel() y[::5] += 3 * (0.5 - rng.rand(16)) # Añadir ruido # Dividir los datos en entrenamiento y evaluación x_train, x_eval, y_train, y_eval = train_test_split(X, y, test_size=0.35, random_state=1982) # Definir modelos con distintos niveles de complejidad regr_underfit = DecisionTreeRegressor(max_depth=1) # Underfitting regr_overfit = DecisionTreeRegressor(max_depth=10) # Overfitting # Entrenar los modelos regr_underfit.fit(x_train, y_train) regr_overfit.fit(x_train, y_train) # Generar predicciones X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis] y_underfit = regr_underfit.predict(X_test) y_overfit = regr_overfit.predict(X_test) # Visualización de resultados fig, ax = plt.subplots(figsize=(12, 6)) plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="Datos") plt.plot(X_test, y_underfit, color="red", linestyle="--", label="Underfitting (max_depth=1)", linewidth=2) plt.plot(X_test, y_overfit, color="green", linestyle=":", label="Overfitting (max_depth=10)", linewidth=2) # Etiquetas y leyenda plt.xlabel("Datos") plt.ylabel("Objetivo") plt.title("Ajuste de Árbol de Decisión en Datos Sinusoidales") plt.legend() plt.show()

In [17]:

# Crear un DataFrame para almacenar los resultados del modelo
results = pd.DataFrame({
    'Model': ['Decision Tree (Underfitting - max_depth=1)', 'Decision Tree (Overfitting - max_depth=10)'],
    'Train Score': [regr_underfit.score(x_train, y_train), regr_overfit.score(x_train, y_train)],
    'Test Score': [regr_underfit.score(x_eval, y_eval), regr_overfit.score(x_eval, y_eval)]
})

# Mostrar resultados
results

# Crear un DataFrame para almacenar los resultados del modelo results = pd.DataFrame({ 'Model': ['Decision Tree (Underfitting - max_depth=1)', 'Decision Tree (Overfitting - max_depth=10)'], 'Train Score': [regr_underfit.score(x_train, y_train), regr_overfit.score(x_train, y_train)], 'Test Score': [regr_underfit.score(x_eval, y_eval), regr_overfit.score(x_eval, y_eval)] }) # Mostrar resultados results

Out[17]:

	Model	Train Score	Test Score
0	Decision Tree (Underfitting - max_depth=1)	0.600781	0.741027
1	Decision Tree (Overfitting - max_depth=10)	1.000000	0.661186

• Underfitting (max_depth=1): La puntuación en entrenamiento es baja (0.600781), indicando que el modelo es demasiado simple y no captura bien los patrones. La puntuación en prueba es algo mejor (0.741027) pero sigue siendo baja, característico de un modelo que no se ajusta bien a los datos.

• Overfitting (max_depth=10): La puntuación en entrenamiento es perfecta (1.000000), pero baja en prueba (0.661186), lo que sugiere que el modelo ajusta demasiado los datos de entrenamiento, capturando ruido y generalizando mal en nuevos datos.

Conclusión: Un modelo con profundidad intermedia podría mejorar el equilibrio entre ajuste y generalización.

Equilibrio en el Ajuste de Modelos¶

Ahora utilizaremos un conjunto de datos generado con make_classification para ilustrar cómo ajustar la complejidad del modelo y alcanzar un equilibrio en el ajuste. Usando el ejemplo de los Árboles de Decisión, evaluaremos la precisión (score) para diferentes profundidades del árbol en los conjuntos de entrenamiento y prueba.

A continuación, el código:

In [19]:

# Librerías
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import pandas as pd

# Generar conjunto de datos
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, random_state=42)

# Dividir el conjunto de datos en entrenamiento y prueba
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Evaluar modelos con diferentes profundidades
train_scores = []
test_scores = []
depths = range(1, 21)

for depth in depths:
    model = DecisionTreeClassifier(max_depth=depth, random_state=42)
    model.fit(x_train, y_train)
    train_scores.append(model.score(x_train, y_train))
    test_scores.append(model.score(x_test, y_test))

# Graficar resultados
plt.figure(figsize=(12, 6))
plt.plot(depths, train_scores, label='Train Score', marker='o')
plt.plot(depths, test_scores, label='Test Score', marker='o')
plt.xlabel("Profundidad del Árbol")
plt.ylabel("Precisión (Score)")
plt.title("Equilibrio entre Overfitting y Underfitting en Árboles de Decisión")
plt.legend()
plt.show()

# Librerías from sklearn.datasets import make_classification from sklearn.tree import DecisionTreeClassifier from sklearn.model_selection import train_test_split import matplotlib.pyplot as plt import pandas as pd # Generar conjunto de datos X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, random_state=42) # Dividir el conjunto de datos en entrenamiento y prueba x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # Evaluar modelos con diferentes profundidades train_scores = [] test_scores = [] depths = range(1, 21) for depth in depths: model = DecisionTreeClassifier(max_depth=depth, random_state=42) model.fit(x_train, y_train) train_scores.append(model.score(x_train, y_train)) test_scores.append(model.score(x_test, y_test)) # Graficar resultados plt.figure(figsize=(12, 6)) plt.plot(depths, train_scores, label='Train Score', marker='o') plt.plot(depths, test_scores, label='Test Score', marker='o') plt.xlabel("Profundidad del Árbol") plt.ylabel("Precisión (Score)") plt.title("Equilibrio entre Overfitting y Underfitting en Árboles de Decisión") plt.legend() plt.show()

In [20]:

# Resultados en DataFrame para referencia
results_df = pd.DataFrame({
    "Profundidad": depths,
    "Train Score": train_scores,
    "Test Score": test_scores
})
results_df

# Resultados en DataFrame para referencia results_df = pd.DataFrame({ "Profundidad": depths, "Train Score": train_scores, "Test Score": test_scores }) results_df

Out[20]:

	Profundidad	Train Score	Test Score
0	1	0.828571	0.810000
1	2	0.854286	0.860000
2	3	0.907143	0.866667
3	4	0.925714	0.883333
4	5	0.952857	0.886667
5	6	0.978571	0.883333
6	7	0.992857	0.876667
7	8	0.998571	0.876667
8	9	1.000000	0.876667
9	10	1.000000	0.876667
10	11	1.000000	0.876667
11	12	1.000000	0.876667
12	13	1.000000	0.876667
13	14	1.000000	0.876667
14	15	1.000000	0.876667
15	16	1.000000	0.876667
16	17	1.000000	0.876667
17	18	1.000000	0.876667
18	19	1.000000	0.876667
19	20	1.000000	0.876667

Explicación:¶

• Generación de datos: Se crea un conjunto de datos de clasificación con 10 características.
• Evaluación de modelos: Entrenamos árboles de decisión con profundidades de 1 a 20, registrando la precisión en los conjuntos de entrenamiento y prueba.
• Visualización: La gráfica muestra cómo la precisión varía con la profundidad del árbol, ilustrando el equilibrio entre underfitting y overfitting:
  • Profundidades bajas: Underfitting, con baja precisión en ambos conjuntos.
  • Profundidades intermedias: Buen equilibrio entre precisión en entrenamiento y prueba.
  • Profundidades altas: Overfitting, alta precisión en entrenamiento pero disminución en prueba.

La tabla results_df ofrece una referencia rápida para comparar las precisiones obtenidas.

Podemos crear un gráfico similar en Scikit-learn utilizando validation_curve para evaluar el rendimiento en distintas profundidades del modelo.

In [22]:

# Librerías
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split, validation_curve
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

# Generar conjunto de datos
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, random_state=42)

# Dividir el conjunto de datos en entrenamiento y prueba
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Rango de profundidades a evaluar
param_range = np.arange(1, 21)

# Obtener scores de validación para distintas profundidades de árbol
train_scores, test_scores = validation_curve(
    DecisionTreeClassifier(random_state=42),
    X, y,
    param_name="max_depth",
    param_range=param_range,
    cv=5,  # Número de particiones para validación cruzada
    scoring="accuracy"
)

# Calcular promedio y desviación estándar de los scores
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)

# Graficar resultados
plt.figure(figsize=(12, 6))
plt.plot(param_range, train_scores_mean, label="Train Score", color="blue", marker='o')
plt.fill_between(param_range, train_scores_mean - train_scores_std,
                 train_scores_mean + train_scores_std, alpha=0.2, color="blue")
plt.plot(param_range, test_scores_mean, label="Test Score", color="orange", marker='o')
plt.fill_between(param_range, test_scores_mean - test_scores_std,
                 test_scores_mean + test_scores_std, alpha=0.2, color="orange")

plt.xlabel("Profundidad del Árbol")
plt.ylabel("Precisión (Score)")
plt.title("Equilibrio entre Overfitting y Underfitting con Árboles de Decisión")
plt.legend()
plt.show()

# Librerías from sklearn.datasets import make_classification from sklearn.tree import DecisionTreeClassifier from sklearn.model_selection import train_test_split, validation_curve import matplotlib.pyplot as plt import numpy as np import pandas as pd # Generar conjunto de datos X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, random_state=42) # Dividir el conjunto de datos en entrenamiento y prueba x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # Rango de profundidades a evaluar param_range = np.arange(1, 21) # Obtener scores de validación para distintas profundidades de árbol train_scores, test_scores = validation_curve( DecisionTreeClassifier(random_state=42), X, y, param_name="max_depth", param_range=param_range, cv=5, # Número de particiones para validación cruzada scoring="accuracy" ) # Calcular promedio y desviación estándar de los scores train_scores_mean = np.mean(train_scores, axis=1) train_scores_std = np.std(train_scores, axis=1) test_scores_mean = np.mean(test_scores, axis=1) test_scores_std = np.std(test_scores, axis=1) # Graficar resultados plt.figure(figsize=(12, 6)) plt.plot(param_range, train_scores_mean, label="Train Score", color="blue", marker='o') plt.fill_between(param_range, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.2, color="blue") plt.plot(param_range, test_scores_mean, label="Test Score", color="orange", marker='o') plt.fill_between(param_range, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.2, color="orange") plt.xlabel("Profundidad del Árbol") plt.ylabel("Precisión (Score)") plt.title("Equilibrio entre Overfitting y Underfitting con Árboles de Decisión") plt.legend() plt.show()

In [ ]:

# Resultados en DataFrame para referencia
results_df = pd.DataFrame({
    "Profundidad": param_range,
    "Train Score Mean": train_scores_mean,
    "Test Score Mean": test_scores_mean
})
results_df

# Resultados en DataFrame para referencia results_df = pd.DataFrame({ "Profundidad": param_range, "Train Score Mean": train_scores_mean, "Test Score Mean": test_scores_mean }) results_df

Out[ ]:

	Profundidad	Train Score Mean	Test Score Mean
0	1	0.82500	0.812
1	2	0.85000	0.838
2	3	0.88900	0.856
3	4	0.91375	0.886
4	5	0.93750	0.888
5	6	0.95475	0.893
6	7	0.97625	0.900
7	8	0.98675	0.888
8	9	0.99400	0.884
9	10	0.99775	0.882
10	11	0.99925	0.880
11	12	1.00000	0.879
12	13	1.00000	0.879
13	14	1.00000	0.879
14	15	1.00000	0.879
15	16	1.00000	0.879
16	17	1.00000	0.879
17	18	1.00000	0.879
18	19	1.00000	0.879
19	20	1.00000	0.879

Referencias¶

1. Underfitting vs Underfitting
2. Overfitting and Underfitting With Machine Learning Algorithms