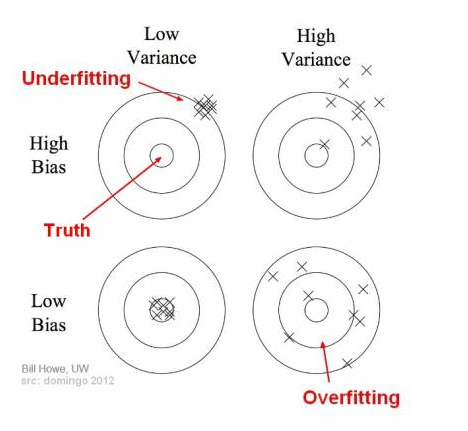
Overfitting II¶

Para mitigar el overfitting, podemos aplicar varias técnicas, entre ellas:

• Recolectar más datos: Ayuda al modelo a generalizar mejor y reducir el ajuste al ruido.
• Regularización: Introducir una penalización a la complejidad del modelo mediante técnicas de regularización.
• Modelos ensamblados: Combinar varios modelos para mejorar la robustez y precisión.
• Validación cruzada: Evaluar el modelo en múltiples particiones para obtener una mejor estimación de su desempeño.
• Optimización de hiperparámetros: Ajustar parámetros con técnicas como grid search para encontrar el equilibrio óptimo entre ajuste y generalización.
• Reducción de la dimensión: Simplificar los datos para disminuir la complejidad del modelo.
• Selección de atributos: Elegir solo las características más relevantes para mejorar la generalización.

A continuación, exploraremos ejemplos de algunos de estos métodos para reducir el sobreajuste.

Validación Cruzada¶

La validación cruzada consiste en dividir el conjunto de datos en $k$ particiones (o pliegues), típicamente entre 5 y 10.

En cada una de las $k$ iteraciones, se selecciona un pliegue diferente como conjunto de evaluación, mientras que los otros $k-1$ pliegues se combinan para formar el conjunto de entrenamiento. Esto implica que, en cada iteración, $(k-1) / k$ de los datos se utiliza para entrenamiento y $1 / k$ para evaluación.

Cada iteración genera una estimación del rendimiento del modelo, proporcionando una medida de su capacidad de generalización. Al finalizar, cada ejemplo ha sido utilizado una vez para evaluación y $k-1$ veces para entrenamiento, permitiendo calcular la media y desviación estándar de la precisión, ofreciendo así una evaluación robusta del modelo.

Veamos un ejemplo en python, ocupando el conjunto de datos make_classification.

In [1]:

# Librerías necesarias
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split, StratifiedKFold
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier
import random

# Configuración de semilla y gráficos
random.seed(1982)
%matplotlib inline
sns.set_palette("deep", desat=0.6)
sns.set_context(rc={"figure.figsize": (12, 4)})

# Generación de datos simulados
X, y = make_classification(n_samples=10000, n_features=100, n_informative=3, n_classes=2, random_state=1982)

# División de datos en entrenamiento y evaluación
x_train, x_eval, y_train, y_eval = train_test_split(X, y, test_size=0.35, random_state=1982)

# Definición del modelo
model = DecisionTreeClassifier(criterion='entropy', max_depth=5)

# Configuración de validación cruzada con 20 pliegues estratificados
skf = StratifiedKFold(n_splits=20)
precision_scores = []

# Validación cruzada
for k, (train_index, test_index) in enumerate(skf.split(x_train, y_train)):
    X_train_fold, X_test_fold = x_train[train_index], x_train[test_index]
    y_train_fold, y_test_fold = y_train[train_index], y_train[test_index]
    
    # Entrenamiento y evaluación en el pliegue actual
    model.fit(X_train_fold, y_train_fold)
    score = model.score(X_test_fold, y_test_fold)
    precision_scores.append(score)
    
    # Imprimir resultados del pliegue
    print(f'Pliegue: {k+1}, Distribución de Clases: {np.bincount(y_train_fold)}, Precisión: {score:.3f}')

# Resultados generales
print("\nPrecisión media de la validación cruzada:", np.mean(precision_scores))

# Librerías necesarias import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns from sklearn.model_selection import train_test_split, StratifiedKFold from sklearn.datasets import make_classification from sklearn.tree import DecisionTreeClassifier import random # Configuración de semilla y gráficos random.seed(1982) %matplotlib inline sns.set_palette("deep", desat=0.6) sns.set_context(rc={"figure.figsize": (12, 4)}) # Generación de datos simulados X, y = make_classification(n_samples=10000, n_features=100, n_informative=3, n_classes=2, random_state=1982) # División de datos en entrenamiento y evaluación x_train, x_eval, y_train, y_eval = train_test_split(X, y, test_size=0.35, random_state=1982) # Definición del modelo model = DecisionTreeClassifier(criterion='entropy', max_depth=5) # Configuración de validación cruzada con 20 pliegues estratificados skf = StratifiedKFold(n_splits=20) precision_scores = [] # Validación cruzada for k, (train_index, test_index) in enumerate(skf.split(x_train, y_train)): X_train_fold, X_test_fold = x_train[train_index], x_train[test_index] y_train_fold, y_test_fold = y_train[train_index], y_train[test_index] # Entrenamiento y evaluación en el pliegue actual model.fit(X_train_fold, y_train_fold) score = model.score(X_test_fold, y_test_fold) precision_scores.append(score) # Imprimir resultados del pliegue print(f'Pliegue: {k+1}, Distribución de Clases: {np.bincount(y_train_fold)}, Precisión: {score:.3f}') # Resultados generales print("\nPrecisión media de la validación cruzada:", np.mean(precision_scores))

Pliegue: 1, Distribución de Clases: [3111 3064], Precisión: 0.929
Pliegue: 2, Distribución de Clases: [3111 3064], Precisión: 0.938
Pliegue: 3, Distribución de Clases: [3111 3064], Precisión: 0.923
Pliegue: 4, Distribución de Clases: [3111 3064], Precisión: 0.945
Pliegue: 5, Distribución de Clases: [3111 3064], Precisión: 0.932
Pliegue: 6, Distribución de Clases: [3111 3064], Precisión: 0.902
Pliegue: 7, Distribución de Clases: [3111 3064], Precisión: 0.920
Pliegue: 8, Distribución de Clases: [3111 3064], Precisión: 0.945
Pliegue: 9, Distribución de Clases: [3111 3064], Precisión: 0.945
Pliegue: 10, Distribución de Clases: [3111 3064], Precisión: 0.926
Pliegue: 11, Distribución de Clases: [3111 3064], Precisión: 0.935
Pliegue: 12, Distribución de Clases: [3111 3064], Precisión: 0.917
Pliegue: 13, Distribución de Clases: [3111 3064], Precisión: 0.908
Pliegue: 14, Distribución de Clases: [3111 3064], Precisión: 0.902
Pliegue: 15, Distribución de Clases: [3111 3064], Precisión: 0.932
Pliegue: 16, Distribución de Clases: [3112 3063], Precisión: 0.938
Pliegue: 17, Distribución de Clases: [3112 3063], Precisión: 0.932
Pliegue: 18, Distribución de Clases: [3112 3063], Precisión: 0.932
Pliegue: 19, Distribución de Clases: [3112 3063], Precisión: 0.923
Pliegue: 20, Distribución de Clases: [3112 3063], Precisión: 0.935

Precisión media de la validación cruzada: 0.9280000000000002

En este ejemplo, utilizamos el iterador StratifiedKFold de Scikit-learn, que realiza validación cruzada estratificada. Esto significa que cada pliegue mantiene la proporción de clases del conjunto de datos original, lo que suele proporcionar estimaciones más precisas del sesgo y la varianza del modelo.

Alternativamente, podríamos utilizar cross_val_score, que facilita la obtención directa de las puntuaciones de precisión para cada pliegue sin necesidad de iterar manualmente.

In [2]:

# Librerías necesarias
import numpy as np
from sklearn.model_selection import cross_val_score, StratifiedKFold
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier

# Generación de datos simulados
X, y = make_classification(n_samples=10000, n_features=100, n_informative=3, n_classes=2, random_state=1982)

# Definición del modelo
model = DecisionTreeClassifier(criterion='entropy', max_depth=5)

# Configuración de validación cruzada con 20 pliegues estratificados
skf = StratifiedKFold(n_splits=20)

# Uso de cross_val_score para obtener precisión en cada pliegue
scores = cross_val_score(model, X, y, cv=skf, scoring='accuracy')

# Resultados
for i, score in enumerate(scores, 1):
    print(f'Pliegue {i}: Precisión = {score:.3f}')

print(f'\nPrecisión media de la validación cruzada: {np.mean(scores):.3f}')
print(f'Desviación estándar de la precisión: {np.std(scores):.3f}')

# Librerías necesarias import numpy as np from sklearn.model_selection import cross_val_score, StratifiedKFold from sklearn.datasets import make_classification from sklearn.tree import DecisionTreeClassifier # Generación de datos simulados X, y = make_classification(n_samples=10000, n_features=100, n_informative=3, n_classes=2, random_state=1982) # Definición del modelo model = DecisionTreeClassifier(criterion='entropy', max_depth=5) # Configuración de validación cruzada con 20 pliegues estratificados skf = StratifiedKFold(n_splits=20) # Uso de cross_val_score para obtener precisión en cada pliegue scores = cross_val_score(model, X, y, cv=skf, scoring='accuracy') # Resultados for i, score in enumerate(scores, 1): print(f'Pliegue {i}: Precisión = {score:.3f}') print(f'\nPrecisión media de la validación cruzada: {np.mean(scores):.3f}') print(f'Desviación estándar de la precisión: {np.std(scores):.3f}')

Pliegue 1: Precisión = 0.928
Pliegue 2: Precisión = 0.914
Pliegue 3: Precisión = 0.916
Pliegue 4: Precisión = 0.938
Pliegue 5: Precisión = 0.924
Pliegue 6: Precisión = 0.938
Pliegue 7: Precisión = 0.924
Pliegue 8: Precisión = 0.938
Pliegue 9: Precisión = 0.936
Pliegue 10: Precisión = 0.908
Pliegue 11: Precisión = 0.936
Pliegue 12: Precisión = 0.938
Pliegue 13: Precisión = 0.934
Pliegue 14: Precisión = 0.922
Pliegue 15: Precisión = 0.930
Pliegue 16: Precisión = 0.928
Pliegue 17: Precisión = 0.924
Pliegue 18: Precisión = 0.926
Pliegue 19: Precisión = 0.936
Pliegue 20: Precisión = 0.920

Precisión media de la validación cruzada: 0.928
Desviación estándar de la precisión: 0.009

Explicación:

• cross_val_score: Realiza la validación cruzada de forma compacta, devolviendo la precisión de cada pliegue en una lista.
• Resultados: Imprimimos la precisión de cada pliegue, la precisión media y la desviación estándar, proporcionando una visión general de la consistencia del modelo en los diferentes pliegues.

Este enfoque es más sencillo y evita la necesidad de un bucle explícito para el cálculo de cada pliegue.

Más Datos y Curvas de Aprendizaje¶

• A veces, reducir el overfitting puede lograrse simplemente con más datos. ¡Dame más datos y te predeciré el futuro!
• Sin embargo, en la práctica, conseguir datos adicionales no suele ser tan sencillo.
• Una técnica útil para entender y reducir el overfitting son las curvas de aprendizaje, que muestran cómo varía la precisión en función del tamaño del conjunto de datos de entrenamiento.

Para graficar las curvas de aprendizaje es necesario ocupar el comando de sklearn llamado learning_curve.

In [3]:

# Librerías necesarias
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import learning_curve
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier
import seaborn as sns

# Configuración de estilo de gráficos
sns.set(style="whitegrid")
plt.figure(figsize=(10, 6))

# Generar un conjunto de datos simulado
X, y = make_classification(n_samples=2000, n_features=20, n_informative=15, random_state=42)

# Definir el modelo de clasificación
model = DecisionTreeClassifier(max_depth=5, random_state=42)

# Calcular las curvas de aprendizaje
train_sizes, train_scores, test_scores = learning_curve(
    model, X, y, cv=5, scoring='accuracy', train_sizes=np.linspace(0.1, 1.0, 10), random_state=42
)

# Calcular media y desviación estándar de las precisiones en cada tamaño de entrenamiento
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)

# Graficar las curvas de aprendizaje
plt.plot(train_sizes, train_mean, 'o-', color="blue", label="Precisión en entrenamiento")
plt.fill_between(train_sizes, train_mean - train_std, train_mean + train_std, alpha=0.2, color="blue")

plt.plot(train_sizes, test_mean, 'o-', color="orange", label="Precisión en validación")
plt.fill_between(train_sizes, test_mean - test_std, test_mean + test_std, alpha=0.2, color="orange")

# Configurar etiquetas y título del gráfico
plt.xlabel("Tamaño del conjunto de entrenamiento")
plt.ylabel("Precisión")
plt.title("Curvas de Aprendizaje")
plt.legend(loc="best")
plt.show()

# Librerías necesarias import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import learning_curve from sklearn.datasets import make_classification from sklearn.tree import DecisionTreeClassifier import seaborn as sns # Configuración de estilo de gráficos sns.set(style="whitegrid") plt.figure(figsize=(10, 6)) # Generar un conjunto de datos simulado X, y = make_classification(n_samples=2000, n_features=20, n_informative=15, random_state=42) # Definir el modelo de clasificación model = DecisionTreeClassifier(max_depth=5, random_state=42) # Calcular las curvas de aprendizaje train_sizes, train_scores, test_scores = learning_curve( model, X, y, cv=5, scoring='accuracy', train_sizes=np.linspace(0.1, 1.0, 10), random_state=42 ) # Calcular media y desviación estándar de las precisiones en cada tamaño de entrenamiento train_mean = np.mean(train_scores, axis=1) train_std = np.std(train_scores, axis=1) test_mean = np.mean(test_scores, axis=1) test_std = np.std(test_scores, axis=1) # Graficar las curvas de aprendizaje plt.plot(train_sizes, train_mean, 'o-', color="blue", label="Precisión en entrenamiento") plt.fill_between(train_sizes, train_mean - train_std, train_mean + train_std, alpha=0.2, color="blue") plt.plot(train_sizes, test_mean, 'o-', color="orange", label="Precisión en validación") plt.fill_between(train_sizes, test_mean - test_std, test_mean + test_std, alpha=0.2, color="orange") # Configurar etiquetas y título del gráfico plt.xlabel("Tamaño del conjunto de entrenamiento") plt.ylabel("Precisión") plt.title("Curvas de Aprendizaje") plt.legend(loc="best") plt.show()

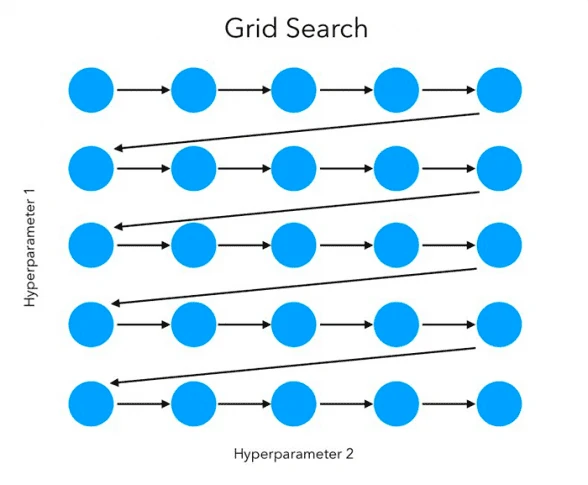
Grid Search¶

La optimización de parámetros es clave para mejorar el rendimiento de los modelos de Machine Learning y reducir el overfitting. Una herramienta común para ello es grid search, que busca de manera exhaustiva la mejor combinación de parámetros para maximizar la precisión del modelo.

Grid search prueba todas las combinaciones especificadas de valores de parámetros y selecciona la que ofrece el mayor rendimiento, evaluando cada opción mediante validación cruzada.

In [5]:

# Importar librerías necesarias
import numpy as np
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier

# Definir el modelo base
model = DecisionTreeClassifier()

# Rango de parámetros para Grid Search
param_grid = {
    'criterion': ['gini', 'entropy'],                    # Función de evaluación para la división de nodos
    'max_depth': [4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 20, 30, 40, 50, 70, 90, 120, 150]  # Profundidades posibles
}

# Configuración y aplicación de Grid Search
gs = GridSearchCV(
    estimator=model, 
    param_grid=param_grid, 
    scoring='accuracy',    # Métrica de evaluación
    cv=5,                  # Número de particiones de validación cruzada
    n_jobs=-1              # Usar todos los núcleos disponibles para acelerar el proceso
)

# Entrenamiento de Grid Search
gs.fit(x_train, y_train)

# Resultados del mejor modelo
print("Mejor precisión en validación cruzada:", gs.best_score_)
print("Mejores parámetros:", gs.best_params_)

# Entrenar y evaluar el mejor modelo en el conjunto de evaluación
mejor_modelo = gs.best_estimator_
mejor_modelo.fit(x_train, y_train)
print("Precisión en el conjunto de evaluación: {:.3f}".format(mejor_modelo.score(x_eval, y_eval)))

# Importar librerías necesarias import numpy as np from sklearn.model_selection import GridSearchCV from sklearn.tree import DecisionTreeClassifier # Definir el modelo base model = DecisionTreeClassifier() # Rango de parámetros para Grid Search param_grid = { 'criterion': ['gini', 'entropy'], # Función de evaluación para la división de nodos 'max_depth': [4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 20, 30, 40, 50, 70, 90, 120, 150] # Profundidades posibles } # Configuración y aplicación de Grid Search gs = GridSearchCV( estimator=model, param_grid=param_grid, scoring='accuracy', # Métrica de evaluación cv=5, # Número de particiones de validación cruzada n_jobs=-1 # Usar todos los núcleos disponibles para acelerar el proceso ) # Entrenamiento de Grid Search gs.fit(x_train, y_train) # Resultados del mejor modelo print("Mejor precisión en validación cruzada:", gs.best_score_) print("Mejores parámetros:", gs.best_params_) # Entrenar y evaluar el mejor modelo en el conjunto de evaluación mejor_modelo = gs.best_estimator_ mejor_modelo.fit(x_train, y_train) print("Precisión en el conjunto de evaluación: {:.3f}".format(mejor_modelo.score(x_eval, y_eval)))

Mejor precisión en validación cruzada: 0.9335384615384615
Mejores parámetros: {'criterion': 'entropy', 'max_depth': 6}
Precisión en el conjunto de evaluación: 0.938

En este ejemplo, utilizamos GridSearchCV para realizar una búsqueda exhaustiva de combinaciones de los parámetros criterion y max_depth, junto con validación cruzada. Este proceso ajusta el modelo iterando sobre todas las combinaciones de valores de estos parámetros.

Al finalizar, imprimimos la mejor precisión obtenida en validación cruzada y los valores óptimos de los parámetros correspondientes. Luego, entrenamos el modelo óptimo en los datos de evaluación y verificamos su rendimiento.

La precisión obtenida en los datos de evaluación es prácticamente idéntica a la de Grid Search, lo que sugiere que el modelo generaliza bien en datos nuevos.

Reducción de Dimensionalidad¶

La reducción de dimensionalidad es una técnica útil para combatir el overfitting al simplificar el modelo eliminando características irrelevantes o redundantes. Esto reduce la complejidad del modelo y ayuda a que generalice mejor en datos nuevos.

Una técnica común para la reducción de dimensionalidad es Análisis de Componentes Principales (PCA), que transforma los datos originales en un nuevo espacio de menor dimensión manteniendo la mayor varianza posible. A continuación, se muestra un ejemplo en Python usando PCA para reducir la dimensionalidad de un conjunto de datos y luego entrenar un modelo de clasificación.

In [6]:

# Importar librerías necesarias
import numpy as np
from sklearn.decomposition import PCA
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score

# Generar datos simulados con 20 características
X, y = make_classification(n_samples=1000, n_features=20, n_informative=10, n_redundant=10, random_state=42)

# Dividir el conjunto de datos en entrenamiento y evaluación
x_train, x_eval, y_train, y_eval = train_test_split(X, y, test_size=0.3, random_state=42)

# Aplicar PCA para reducir las características a 10 componentes principales
pca = PCA(n_components=10)
x_train_pca = pca.fit_transform(x_train)
x_eval_pca = pca.transform(x_eval)

# Definir y entrenar el modelo en los datos reducidos
model = DecisionTreeClassifier(max_depth=5, random_state=42)
model.fit(x_train_pca, y_train)

# Evaluar el modelo en los datos de evaluación
y_pred = model.predict(x_eval_pca)
accuracy = accuracy_score(y_eval, y_pred)

print("Precisión con reducción de dimensionalidad (PCA): {:.3f}".format(accuracy))

# Importar librerías necesarias import numpy as np from sklearn.decomposition import PCA from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import accuracy_score # Generar datos simulados con 20 características X, y = make_classification(n_samples=1000, n_features=20, n_informative=10, n_redundant=10, random_state=42) # Dividir el conjunto de datos en entrenamiento y evaluación x_train, x_eval, y_train, y_eval = train_test_split(X, y, test_size=0.3, random_state=42) # Aplicar PCA para reducir las características a 10 componentes principales pca = PCA(n_components=10) x_train_pca = pca.fit_transform(x_train) x_eval_pca = pca.transform(x_eval) # Definir y entrenar el modelo en los datos reducidos model = DecisionTreeClassifier(max_depth=5, random_state=42) model.fit(x_train_pca, y_train) # Evaluar el modelo en los datos de evaluación y_pred = model.predict(x_eval_pca) accuracy = accuracy_score(y_eval, y_pred) print("Precisión con reducción de dimensionalidad (PCA): {:.3f}".format(accuracy))

Precisión con reducción de dimensionalidad (PCA): 0.827

Explicación

1. Generación de Datos: Se crean datos simulados con 20 características, de las cuales 10 son informativas y 10 redundantes, lo que es común en conjuntos de datos reales.
2. Reducción de Dimensionalidad: Se aplica PCA para reducir las 20 características originales a 10 componentes principales, manteniendo la información más relevante.
3. Entrenamiento del Modelo: Se entrena un DecisionTreeClassifier en los datos reducidos de entrenamiento.
4. Evaluación: Se calcula la precisión del modelo en los datos de evaluación transformados, observando cómo la reducción de dimensionalidad impacta el rendimiento.

Referencias¶

1. K-Fold Cross Validation
2. Cross Validation and Grid Search for Model Selection in Python
3. Feature selection for supervised models using SelectKBest