Funciones¶

Introducción¶

Las funciones en Python son bloques de código que pueden ser llamados en cualquier momento del programa. Estos bloques de código reciben uno o varios argumentos y pueden devolver un valor. Las funciones son muy útiles porque te permiten escribir código una vez y reutilizarlo en distintas partes del programa, lo que puede ahorrar mucho tiempo y esfuerzo.

Formalmente, una función tiene tres componentes importantes:

• los parámetros, que son los valores que recibe la función como entrada;
• el código de la función, que son las operaciones que hace la función; y
• el resultado (o valor de retorno), que es el valor final que entrega la función.

En esencia, una función es un mini programa. Sus tres componentes son análogos a la entrada, el proceso y la salida de un programa.

Definición de funciones

Las funciones en Python lucen de la siguiente forma:

def nombre(parametro_1,...,parametro_n):
    """
    Descripcion de la funcion (opcional)
    """
    # código de la función
    resultado = operacion(parametro_1,...,parametro_n)
    return resultado # output de la funcion

Se utiliza la palabra clave def seguida del nombre de la función, los parámetros que recibe entre paréntesis y dos puntos :. El cuerpo de la función va indentado y puede contener cualquier código que se quiera ejecutar. Para devolver un valor se utiliza la palabra clave return.

In [1]:

def suma(a, b):
    return a + b

resultado = suma(3, 5)
print(resultado)

def suma(a, b): return a + b resultado = suma(3, 5) print(resultado)

8

En este ejemplo se define una función llamada suma que recibe dos parámetros a y b y devuelve la suma de ambos. Se llama a la función con los valores 3 y 5 y se almacena el resultado en una variable llamada resultado. Finalmente, se imprime el valor de resultado.

Por otro lado, dado que no se especifica el tipo de datos, podemos sumar dos strings

In [3]:

resultado = suma("Hola ","Mundo")
print(resultado)

resultado = suma("Hola ","Mundo") print(resultado)

Hola Mundo

Por lo que se debe tener cuidado tanto con el nombre de la función (se espera que pueda resumir la funcion en una o dos palabras) y el tipo de argumentos que queremos que reciba.

Las funciones también pueden tener argumentos opcionales que tienen un valor por defecto. Para definir un argumento opcional se utiliza el operador = para asignarle un valor por defecto. El valor por defecto se utiliza si el argumento no es especificado al llamar a la función.

In [4]:

def saludo(nombre, saludo="Hola"):
    print(saludo, nombre)

saludo("Pedro")
saludo("Maria", "Buenos días")

def saludo(nombre, saludo="Hola"): print(saludo, nombre) saludo("Pedro") saludo("Maria", "Buenos días")

Hola Pedro
Buenos días Maria

En este ejemplo se define una función llamada saludo que recibe dos argumentos, nombre y saludo. El argumento saludo tiene un valor por defecto de "Hola". La función imprime el mensaje de saludo utilizando los valores de saludo y nombre. Se llama a la función con diferentes valores de argumentos.

A continuación, se creará la función factorial, la cual entregará el factorial de un número entero no negativo.

In [5]:

def factorial(n):
    """
    factorial de un numero entero no negativo
    """
    f = 1
    for i in range(1, n + 1):
        f *= i
    return f

def factorial(n): """ factorial de un numero entero no negativo """ f = 1 for i in range(1, n + 1): f *= i return f

En este ejemplo, el resultado que entrega una llamada a la función es el valor que tiene la variable f al llegar a la última línea de la función.

Una vez creada, la función puede ser usada como cualquier otra, todas las veces que sea necesario:

In [6]:

print(factorial(0))

print(factorial(0))

1

In [7]:

print(factorial(2) + factorial(5))

print(factorial(2) + factorial(5))

122

Las variables que son creadas dentro de la función (incluyendo los parámetros y el resultado) se llaman variables locales, y sólo son visibles dentro de la función, no desde el resto del programa.

Por otra parte, las variables creadas fuera de alguna función se llaman variables globales, y son visibles desde cualquier parte del programa. Sin embargo, su valor no puede ser modificado, ya que una asignación crearía una variable local del mismo nombre.

In [8]:

# ejemplo variable global

valor = 10 # variable global

def funcion_01(x):
    return valor*x

# ejemplo variable global valor = 10 # variable global def funcion_01(x): return valor*x

In [27]:

print(funcion_01(5))

print(funcion_01(5))

50

In [10]:

# ejemplo variable local

def funcion_02(x,valor):
    
    resultado = valor*x
    
    return resultado

# ejemplo variable local def funcion_02(x,valor): resultado = valor*x return resultado

In [28]:

print(funcion_02(5,2))

print(funcion_02(5,2))

10

Nota: Dependiendo del uso que le dé a su código es que ocupará variables globales o no, sin embargo, es preferible definir su función solo con variables locales, puesto que esto deja explícita la dependencia de dicha variable dentro de su función objetivo.

Por otro lado, existen funciones que no necesariamente reciben argumentos.

In [12]:

def imprimir_pantalla():
    return "Mensaje random"

def imprimir_pantalla(): return "Mensaje random"

In [13]:

imprimir_pantalla()

imprimir_pantalla()

Out[13]:

'Mensaje random'

También, existen funciones que no retornan valores:

In [14]:

def imprimir_nombre(nombre):
    print(nombre)

def imprimir_nombre(nombre): print(nombre)

In [15]:

imprimir_nombre("nombre_01")

imprimir_nombre("nombre_01")

nombre_01

Formas de escribir una función¶

Recursion¶

Una función que se llama a sí misma se conoce como función recursiva y este proceso se llama recursividad. Cada función recursiva debe tener una condición base que detenga la recursividad o, de lo contrario, la función se llama a sí misma infinitamente.

In [16]:

# funcion factorial (recursivo)

def factorial(n):
    """
    Funcion factorial de manera recursiva
    """
    if n == 1:
        return 1
    else:
        return (n * factorial(n-1))

# funcion factorial (recursivo) def factorial(n): """ Funcion factorial de manera recursiva """ if n == 1: return 1 else: return (n * factorial(n-1))

Analicemos recursivamente el factorial del número $3$.

In [17]:

num = 3
print(f"El factorial de {num} es {factorial(num)}")

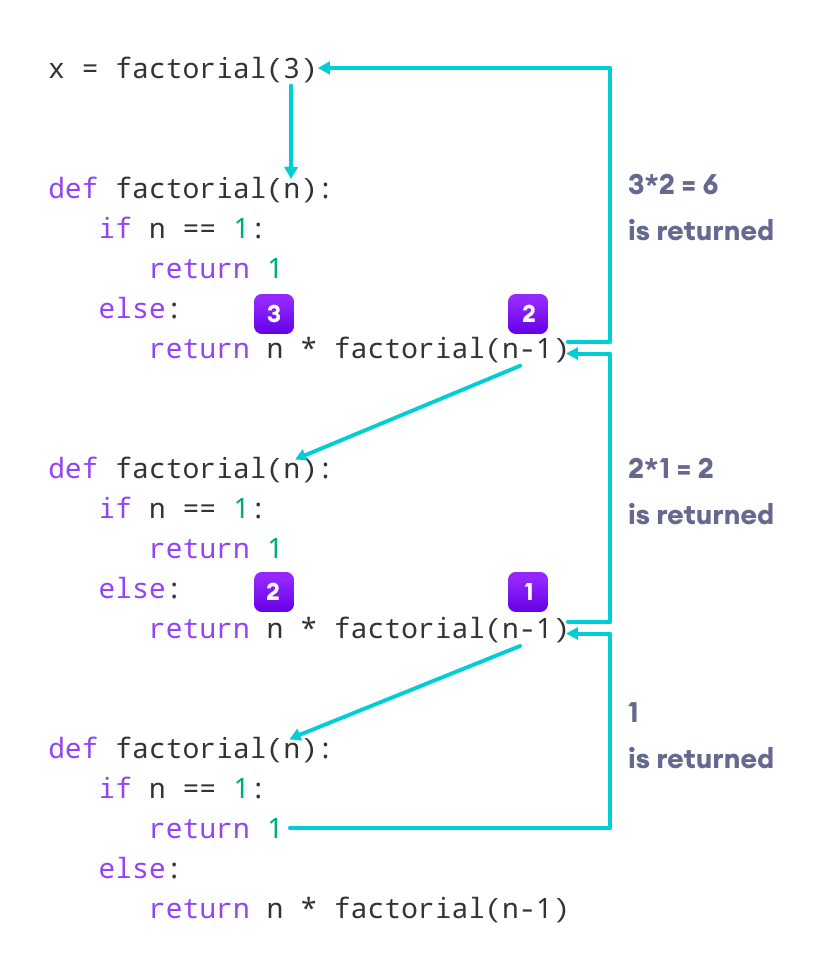
num = 3 print(f"El factorial de {num} es {factorial(num)}")

El factorial de 3 es 6

Lambda¶

En Python, puedes definir funciones sin nombre utilizando funciones lambda o, como también se les conoce, funciones anónimas. Estas funciones son útiles para realizar operaciones simples en una sola línea de código. Para crear una función lambda, se utiliza la palabra clave lambda. A continuación, te presento una comparación entre una función definida de manera convencional y una función lambda:

Función Definida de Manera Convencional:

In [1]:

def cuadrado_normal(x):
    """
    Función que eleva al cuadrado un número.
    """
    return x ** 2

# Llamamos a la función convencional
resultado_normal = cuadrado_normal(5)
print(resultado_normal)

def cuadrado_normal(x): """ Función que eleva al cuadrado un número. """ return x ** 2 # Llamamos a la función convencional resultado_normal = cuadrado_normal(5) print(resultado_normal)

25

Función Lambda:

In [2]:

# Definimos una función lambda para elevar al cuadrado un número
cuadrado = lambda x: x ** 2

# Llamamos a la función lambda
resultado_lambda = cuadrado(5)
print(resultado_lambda)

# Definimos una función lambda para elevar al cuadrado un número cuadrado = lambda x: x ** 2 # Llamamos a la función lambda resultado_lambda = cuadrado(5) print(resultado_lambda)

25

Explicación:

• En el primer ejemplo, se define una función convencional llamada cuadrado_normal que toma un argumento x y devuelve el cuadrado de x utilizando la declaración return.

• En el segundo ejemplo, se crea una función lambda que realiza la misma operación. La función lambda se define como lambda x: x ** 2, donde x es el argumento de entrada y x ** 2 es la expresión que se evalúa y devuelve.

• Luego, llamamos tanto a la función convencional como a la función lambda con un valor de 5 como argumento, y guardamos los resultados en las variables resultado_normal y resultado_lambda, respectivamente.

• Finalmente, imprimimos los resultados, que serán 25 tanto para la función convencional como para la función lambda, ya que ambas calculan el cuadrado de 5.

Utilizando *args y **kwargs¶

En Python, puedes utilizar *args y **kwargs para manejar un número variable de argumentos en una función. Estos nombres, args y kwargs, son convenciones comunes, pero en realidad puedes nombrarlos como desees. Ahora, profundicemos en estos conceptos:

• *args: Es una convención para indicar que se acepta un número variable de argumentos no nombrados (posicionales). Los argumentos se almacenan en una tupla.

• **kwargs: Es una convención para indicar que se acepta un número variable de argumentos con nombre. Los argumentos se almacenan en un diccionario, donde las claves se convierten en los nombres de los parámetros y los valores son los argumentos asociados.

Usando *args:

In [3]:

def sumar_numeros(*numeros):
    suma = 0
    for numero in numeros:
        suma += numero
    return suma

resultado = sumar_numeros(1, 2, 3, 4)
print(resultado)

def sumar_numeros(*numeros): suma = 0 for numero in numeros: suma += numero return suma resultado = sumar_numeros(1, 2, 3, 4) print(resultado)

10

En el primer ejemplo, se define la función sumar_numeros, que toma un número variable de argumentos no nombrados. La función suma todos los argumentos recibidos y devuelve el resultado. En este caso, llamamos a la función con los números 1, 2, 3, 4, y la suma se almacena en resultado.

**Usando **kwargs:**

In [4]:

def imprimir_datos(**datos):
    for llave, valor in datos.items():
        print(llave, ":", valor)

imprimir_datos(nombre="Juan", edad=25, ciudad="Lima")

def imprimir_datos(**datos): for llave, valor in datos.items(): print(llave, ":", valor) imprimir_datos(nombre="Juan", edad=25, ciudad="Lima")

nombre : Juan
edad : 25
ciudad : Lima

En el segundo ejemplo, se define la función imprimir_datos, que toma un número variable de argumentos con nombre. La función itera a través del diccionario datos y muestra las claves y sus valores asociados. Llamamos a la función con argumentos con nombre, como "nombre", "edad" y "ciudad", y se imprime la información correspondiente.

Nota: Es importante recordar que aunque *args y **kwargs son útiles, se recomienda ser explícito en la definición de tus funciones siempre que sea posible para hacer el código más legible y mantenible.

Ejercicios¶

Ejercicio 01

Escriba una función que se llame saludar que reciba como input un string s y devuelva como output "Hola + valor de s".

• Ejemplo: saludar("mundo") = "Hola mundo"

In [ ]:

# respuesta

# respuesta

Ejercicio 02

Escriba una función que se llame es_par que reciba como input un número entero n y devuelva como output True si el número es par, y False en otro caso.

• Ejemplo:
  • es_par(4) = True
  • es_par(3) = False

In [ ]:

# respuesta

# respuesta

Ejercicio 03

Escriba la función invertir_digitos(n) que reciba un número entero n y entregue como resultado el número n con los dígitos en el orden inverso:

terminal
 >>> invertir_digitos(142)
241

A continuación, escriba un programa que indique si el número ingresado es palíndromo o no, usando la función invertir_digitos:

terminal
Ingrese n: 81418
Es palíndromo

In [ ]:

# respuesta

# respuesta

Ejercicio 04

Muchos de estos programas sólo tenían pequeñas diferencias entre ellos, por lo que había que repetir mucho código al escribirlos. En este ejercicio, usted deberá implementar algunos de esos programas como funciones, reutilizando componentes para evitar escribir código repetido.

Ejercicio 041

Escriba la función es_divisible(n, d) que indique si n es divisible por d:

>>> es_divisible(15, 5)
True
>>> es_divisible(15, 6)
False

Ejercicio 042

Usando la función es_divisible, escriba una función es_primo(n) que determine si un número es primo o no:

>>> es_primo(17)
True
>>> es_primo(221)
False

Ejercicio 043

Usando la función es_primo, escriba la función i_esimo_primo(i) que entregue el i-ésimo número primo.

>>> i_esimo_primo(1)
2
>>> i_esimo_primo(20)
71

Ejercicio 044

Usando las funciones anteriores, escriba la función primeros_primos(m) que entregue una lista de los primeros m números primos:

>>> primeros_primos(10)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]

Ejercicio 045

Usando las funciones anteriores, escriba la función primos_hasta(m) que entregue una lista de los primos menores o iguales que m:

>>> primos_hasta(19)
[2, 3, 5, 7, 11, 13, 17, 19]

Ejercicio 046

Un primo de Mersenne es un número primo de la forma $2p−1$. Una propiedad conocida de los primos de Mersenne es que $p$ debe ser también un número primo.

Escriba la función mersenne que pregunte al usuario un número $n$, y muestre como salida los primeros n primos de Mersenne:

>>> mersenne(5)
3
7
31
127
8191

In [ ]:

# respuesta

# respuesta

Ejercicio 05

La suma natural de los primeros n números naturales esta dado por: $$\displaystyle S = \sum_{k=1}^{n} k = 1 +2 +3 +...+n = \dfrac{n(n+1)}{2} $$

Escriba una función que se llame suma_numeros_naturales que reciba como input un número entero n y devuelva como output la suma de los primeros n números naturales.

Para esto:

• a) Programe la función ocupando la fórmula manual: $S = 1+2+3+..+n$
• b) Programe la función ocupando la fórmula cerrada: $S =\dfrac{n(n+1)}{2} $

Ejemplo:

• suma_numeros_naturales(1) = 1
• suma_numeros_naturales(10) = 55
• suma_numeros_naturales(100) = 5050

In [ ]:

# respuesta

# respuesta

Ejercicio 06

En los siglos XVII y XVIII, James Gregory y Gottfried Leibniz descubrieron una serie infinita que sirve para calcular $\pi$:

$$\displaystyle \pi = 4 \sum_{k=1}^{\infty}\dfrac{(-1)^{k+1}}{2k-1} = 4(1-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7} + ...) $$

Desarolle un programa para estimar el valor de $\pi$ ocupando el método de Leibniz, donde la entrada del programa debe ser un número entero $n$ que indique cuántos términos de la suma se utilizará.

• Ejemplo:
  • calcular_pi(3) = 3.466666666666667
  • calcular_pi(1000) = 3.140592653839794

In [ ]:

# respuesta

# respuesta

Ejercicio 07

Euler realizó varios aportes en relación a $e$, pero no fue hasta 1748 cuando publicó su Introductio in analysin infinitorum que dio un tratamiento definitivo a las ideas sobre $e$. Allí mostró que:

En los siglos XVII y XVIII, James Gregory y Gottfried Leibniz descubrieron una serie infinita que sirve para calcular π:

$$\displaystyle e = \sum_{k=0}^{\infty}\dfrac{1}{k!} = 1+\dfrac{1}{2!}+\dfrac{1}{3!}+\dfrac{1}{4!} + ... $$

Desarolle un programa para estimar el valor de $e$ ocupando el método de Euler, donde la entrada del programa debe ser un número entero $n$ que indique cuántos términos de la suma se utilizará.

Para esto:

• a) Defina la función factorial, donde la entrada sea un número natural $n$ y la salida sea el factorial de dicho número.

  • Ejemplo: factorial(3) =3, factorial(5) = 120

• b) Ocupe la función factorial dentro de la función calcular_e.

  • Ejemplo: calcular_e(3) = 2.6666666666666665, calcular_e(1000) = 2.7182818284590455

In [ ]:

# respuesta

# respuesta

Ejercicio 08

Sea $\sigma(n)$ definido como la suma de los divisores propios de $n$ (números menores que n que se dividen en $n$).

Los números amigos son enteros positivos $n_1$ y $n_2$ tales que la suma de los divisores propios de uno es igual al otro número y viceversa, es decir, $\sigma(n_1)=\sigma(n_2)$ y $\sigma(n_2)=\sigma(n_1)$.

Por ejemplo, los números 220 y 284 son números amigos.

• los divisores propios de 220 son 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110; por lo tanto $\sigma(220) = 284$.
• los divisores propios de 284 son 1, 2, 4, 71 y 142; entonces $\sigma(284) = 220$.

Implemente una función llamada amigos cuyo input sean dos números naturales $n_1$ y $n_2$, cuyo output sea verifique si los números son amigos o no.

Para esto:

• a) Defina la función divisores_propios, donde la entrada sea un número natural $n$ y la salida sea una lista con los divisores propios de dicho número.

  • Ejemplo: divisores_propios(220) = [1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110], divisores_propios(284) = [1, 2, 4, 71 y 142]

• b) Ocupe la función divisores_propios dentro de la función amigos.

  • Ejemplo: amigos(220,284) = True, amigos(6,5) = False

In [ ]:

# respuesta

# respuesta

Ejercicio 09

La conjetura de Collatz, conocida también como conjetura $3n+1$ o conjetura de Ulam (entre otros nombres), fue enunciada por el matemático Lothar Collatz en 1937, y a la fecha no se ha resuelto.

Sea la siguiente operación, aplicable a cualquier número entero positivo:

• Si el número es par, se divide entre 2.
• Si el número es impar, se multiplica por 3 y se suma 1.

La conjetura dice que siempre alcanzaremos el 1 (y por tanto el ciclo 4, 2, 1) para cualquier número con el que comencemos.

Implemente una función llamada collatz cuyo input sea un número natural positivo $N$ y como output devulva la secuencia de números hasta llegar a 1.

• Ejemplo: collatz(9) = [9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1]

In [ ]:

# respuesta

# respuesta

Ejercicio 10

La conjetura de Goldbach es uno de los problemas abiertos más antiguos en matemáticas. Concretamente, G.H. Hardy, en 1921, en su famoso discurso pronunciado en la Sociedad Matemática de Copenhague, comentó que probablemente la conjetura de Goldbach no es solo uno de los problemas no resueltos más difíciles de la teoría de números, sino de todas las matemáticas. Su enunciado es el siguiente:

Todo número par mayor que 2 puede escribirse como suma de dos números primos - Christian Goldbach (1742)

Implemente una función llamada goldbach cuyo input sea un número natural positivo $n$ y como output devuelva la suma de dos primos ($n_1$ y $n_2$) tal que: $n_1+n_2=n$.

Para esto:

• a) Defina la función es_primo, donde la entrada sea un número natural $n$ y la salida sea True si el número es primo y False en otro caso.

  • Ejemplo: es_primo(3) = True, es_primo(4) = False

• b) Defina la función lista_de_primos, donde la entrada sea un número natural par $n$ mayor que dos y la salida sea una lista con todos los número primos entre 2 y $n$.

  • Ejemplo: lista_de_primos(4) = [2,3], lista_de_primos(6) = [2,3,5], lista_de_primos(8) = [2,3,5,7]

• c) Ocupe la función lista_de_primos dentro de la función goldbash.

• Ejemplo: goldbash(4) = (2,2), goldbash(6) = (3,3) , goldbash(8) = (3,5)

Ejercicio 11

El producto interno de dos listas de números es la suma de los productos de los términos correspondientes de ambas.

Por ejemplo, si:

a = [5, 1, 6]
b = [1, -2, 8]

entonces el producto interno entre $a$ y $b$ es:

(5 * 1) + (1 * -2) + (6 * 8)

1. Escriba la función producto_interno(a, b) que entregue el producto interno de a y b:

   >>> a = [7, 1, 4, 9, 8]
   >>> b = range(5)
   >>> producto_interno(a, b)
   68
   

2. Dos listas de números son ortogonales si su producto interno es cero. Escriba la función son_ortogonales(a, b) que indique si a y b son ortogonales:

   >>> son_ortogonales([2, 1], [-3, 6])
   True
   

In [ ]:

# respuesta

# respuesta

Ejercicio 12

Una fecha puede ser representada como una tupla (anno, mes, dia).

1. Escriba la función dia_siguiente(f) que reciba como parámetro una fecha f y entegue cuál es la fecha siguiente:

   >>> dia_siguiente((2011, 4, 11))
   (2011, 4, 12)
   >>> dia_siguiente((2011, 4, 30))
   (2011, 5, 1)
   >>> dia_siguiente((2011, 12, 31))
   (2012, 1, 1)
   

   Como recomendación, dentro de su función use una lista con la cantidad de días que tiene cada mes:

   dias_mes = [31, 28, 31, 30,
           31, 30, 31, 31,
           30, 31, 30, 31]
   

2. Escriba la función dias_entre(f1, f2) que retorne la cantidad de días que han transcurrido entre las fechas f1 y f2:

   >>> hoy = (2011, 4, 11)
   >>> navidad = (2011, 12, 25)
   >>> dias_entre(hoy, navidad)
   258
   >>> dias_entre(hoy, hoy)
   0
   

In [ ]:

# respuesta

# respuesta

Ejercicio 13

El conjunto potencia de un conjunto $S$ es el conjunto de todos los subconjuntos de $S$.

Por ejemplo, el conjunto potencia de $\{1,2,3\}$ es:

$$\{\emptyset,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}\}$$

En Python, un conjunto no puede contener a otros conjuntos, ya que no puede tener elementos mutables, y los conjuntos lo son:

>>> a = set()
>>> a.add({1, 2})        # :(
Traceback (most recent call last):
  File "<console>", line 1, in <module>
TypeError: unhashable type: 'set'

Lo que sí podemos crear es una lista de conjuntos:

>>> l = list()
>>> l.append({1, 2})     # :)
>>> l
[set([1, 2])]

Escriba la función conjunto_potencia(s) que reciba como parámetro un conjunto cualquiera s y retorne su «lista potencia» (la lista de todos sus subconjuntos):

>>> conjunto_potencia({6, 1, 4})
[set(), set([6]), set([1]), set([4]), set([6, 1]), set([6, 4]), set([1, 4]), set([6, 1, 4])]

In [ ]:

# respuesta

# respuesta

Ejercicio 14

Para este ejercicio considere lo siguiente:

Para obtener la lista de palabras de la oración, puede usar el método split de los strings:

>>> s = 'el gato y el pato'
>>> s.split()
['el', 'gato', 'y', 'el', 'pato']

Para obtener un string en minúsculas, puede usar el método lower:

>>> s = 'Venezuela'
>>> s.lower()
'venezuela'

1. Escriba la función contar_letras(oracion) que retorne un diccionario asociando a cada letra la cantidad de veces que aparece en la oracion:

   >>> contar_letras('El elefante avanza hacia Asia')
   {'a': 8, 'c': 1, 'e': 4, 'f': 1, 'h': 1, 'i': 2, 'l': 2, 'n': 2, 's': 1, 't': 1, 'v': 1, 'z': 1}
   

   Cada valor del diccionario debe considerar tanto las apariciones en mayúscula como en minúscula de la letra correspondiente. Los espacios deben ser ignorados.

2. Escriba la función contar_vocales(oracion) que retorne un diccionario asociando a cada vocal la cantidad de veces que aparece en la oracion. Si una vocal no aparece en la oración, de todos modos debe estar en el diccionario asociada al valor 0:

   >>> contar_vocales('El elefante avanza hacia Asia')
   {'a': 8, 'e': 4, 'i': 2, 'o': 0, 'u': 0}
   

3. Escriba la función contar_iniciales(oracion) que retorne un diccionario asociando a cada letra la cantidad de veces que aparece al principio de una palabra:

   >>> contar_iniciales('El elefante avanza hacia Asia')
   {'e': 2, 'h': 1, 'a': 2}
   >>> contar_iniciales('Varias vacas vuelan sobre Venezuela')
   {'s': 1', 'v': 4}
   

4. Escriba la función obtener_largo_palabras(oracion) que retorne un diccionario asociando a cada palabra su cantidad de letras:

   >>> obtener_largo_palabras('el gato y el pato son amigos')
   {'el': 2, 'son': 3, 'gato': 4, 'y': 1, 'amigos': 6, 'pato': 4}
   

5. Escriba la función contar_palabras(oracion) que retorne un diccionario asociando a cada palabra la cantidad de veces que aparece en la oración:

   >>> contar_palabras('El sobre esta sobre el pupitre')
   {'sobre': 2, 'pupitre': 1, 'el': 2, 'esta': 1}
   

6. Escriba la función palabras_repetidas(oracion) que retorne una lista con las palabras que están repetidas:

   >>> palabras_repetidas('El partido termino cero a cero')
   ['cero']
   >>> palabras_repetidas('El sobre esta sobre el mueble')
   ['el', 'sobre']
   >>> palabras_repetidas('Ay, ahi no hay pan')
   []
   

In [ ]:

# respuesta

# respuesta