💻 Programación¶
Introducción¶
“Se dice que uno no comprende verdaderamente algo hasta que puede explicárselo a otro. En realidad, uno no lo entiende completamente hasta que puede explicárselo a una computadora.” -- Donald Knuth
Si tuviéramos que resumir el propósito de la programación en una frase, sería:
Automatizar tareas para que la computadora las realice por nosotros.
Las computadoras son expertas en llevar a cabo tareas rutinarias. Idealmente, cualquier labor tediosa y repetitiva debería ser delegada a una computadora, permitiendo así que los humanos se enfoquen en los problemas verdaderamente interesantes: aquellos que demandan creatividad, pensamiento crítico y subjetividad.
La programación es el proceso de traducir un enfoque para resolver problemas en términos comprensibles para la computadora.
Además, la programación abarca una amplia gama de lenguajes y paradigmas, cada uno con sus propias características y aplicaciones. Desde los clásicos como C y Java hasta los modernos como Python y JavaScript, cada lenguaje tiene sus fortalezas y debilidades, y la elección del lenguaje adecuado depende del contexto y los requisitos del proyecto.
La programación no se limita solo a escribir código. También implica planificación, diseño y depuración de software. Los programadores deben comprender los requisitos del usuario, diseñar soluciones eficientes y depurar errores para garantizar que el software funcione correctamente.
Algoritmos¶

“La informática se trata de computadores tanto como la astronomía se trata de telescopios.” -- Edsger Dijkstra
Al diseñar un programa, el desafío principal es crear y describir un procedimiento que esté completamente bien definido, sin ambigüedades, y que efectivamente resuelva el problema.
Por tanto, la programación no se centra tanto en los computadores como en resolver problemas de manera estructurada. Su objeto de estudio principal son los algoritmos.
Un algoritmo es un procedimiento bien definido para resolver un problema. Todos utilizamos algoritmos a diario, incluso sin darnos cuenta:
a) Receta de cocina
Una receta de cocina es un ejemplo de algoritmo; aunque algunos pasos puedan parecer ambiguos (¿cuánto es «una pizca de sal»? ¿qué significa «agregar a gusto»?), en general las instrucciones están lo suficientemente bien definidas para seguirlas sin problemas.
La entrada de una receta son los ingredientes y ciertos datos como: ¿para cuántas personas se está cocinando? El proceso es la serie de pasos para manipular los ingredientes. La salida es el plato terminado.
En principio, si una receta está suficientemente bien explicada, cualquiera podría preparar el plato incluso sin conocimientos previos de cocina.
b) Método de multiplicación
El método para multiplicar números a mano que aprendemos en la escuela es otro ejemplo de algoritmo. Siguiendo paso a paso el procedimiento, siempre obtendremos el producto.
La entrada del algoritmo de multiplicación son los dos factores. El proceso consiste en una secuencia de pasos donde los dígitos se multiplican, las reservas se suman, y los productos intermedios se suman finalmente. La salida del algoritmo es el producto obtenido.
Componentes de un algoritmo¶
Conceptualmente, un algoritmo consta de tres elementos principales:
- Entrada: Representa los datos iniciales o inputs que el algoritmo utilizará para llevar a cabo su tarea.
- Proceso: Consiste en la serie de pasos lógicos y operaciones que el algoritmo realiza utilizando la entrada para producir un resultado.
- Salida: Es el resultado final o output que proporciona el algoritmo después de ejecutar el proceso.
El proceso se describe mediante una secuencia ordenada de instrucciones. Además, puede incluir estructuras como ciclos, que repiten un conjunto de instrucciones un número determinado de veces, y condicionales, que determinan qué conjunto de instrucciones se ejecutarán según ciertas condiciones.
Cómo describir un algoritmo¶
Consideremos un ejemplo sencillo: un algoritmo para resolver ecuaciones cuadráticas.
Una ecuación cuadrática es una ecuación de la forma $ax^2+bx+c=0$, donde $a, b$ y $c$ son datos dados, con $a\neq0$, y $x$ es la incógnita cuyo valor que se desea determinar.
Por ejemplo, $2x^2−5x+2=0$ es una ecuación cuadrática con $a=2$, $b=−5$ y $c=2$. Sus soluciones son $x_1=1/2$ y $x_2=2$, como se puede comprobar fácilmente al reemplazar estos valores en la ecuación. El problema es cómo obtener estos valores en primer lugar.
El problema computacional de resolver una ecuación cuadrática puede ser planteado así:
Dados $a, b$ y $c$, entontrar los valores reales de $x$ que satisfacen $ax^2+bx+c=0$.
La entrada del algoritmo, pues, son los valores $a, b$ y $c$, y la salida son las raíces reales $x$ (que pueden ser cero, una o dos) de la ecuación. En un programa computacional, los valores de $a, b$ y $c$ deberían ser ingresados usando el teclado, y las soluciones $x$ deberían ser mostradas a continuación en la pantalla.
Al estudiar álgebra aprendemos un algoritmo para resolver este problema. Es lo suficientemente detallado para que pueda usarlo cualquier persona, incluso sin saber qué es una ecuación cuadrática, o para que lo pueda hacer un computador. A continuación veremos algunas maneras de describir el procedimiento.
Lenguaje natural
Durante el proceso mental de diseñar un algoritmo, es común pensar y describir los pasos en la misma manera en que hablamos a diario. Por ejemplo:
Teniendo los valores de $a, b$ y $c$, calcular el discriminante $D=b^2−4ac$. Si es discriminante es negativo, entonces la ecuación no tiene soluciones reales. Si es discriminante es igual a cero, entonces la ecuación tiene una única solución real, que es $x=−b/2a$. Si el discriminante es positivo, entonces la ecuación tiene dos soluciones reales, que son $x_1=(−b−\sqrt{D})/2a$ y $x_2=(−b+\sqrt{D})/2a$.
Esta manera de expresar un algoritmo no es ideal, ya que el lenguaje natural es:
- impreciso: puede tener ambigüedades;
- no universal: personas distintas describirán el proceso de maneras distintas; y
- no estructurado: la descripción no está expresada en función de componentes simples.
Aún así, es posible identificar los pasos del algoritmo. Por ejemplo, hay que evaluar la expresión $b^2−4ac$, y ponerle el nombre $D$ a su resultado. Esto se llama asignación, y es un tipo de instrucción que aparece en casi todos los algoritmos. Después de eso, el algoritmo puede usar el nombre $D$ para referirse al valor calculado.
Diagrama de flujo Un diagrama de flujo es una representación gráfica de un algoritmo. Los pasos son representados por varios tipos de bloques, y el flujo de ejecución es indicado por flechas que conectan los bloques:
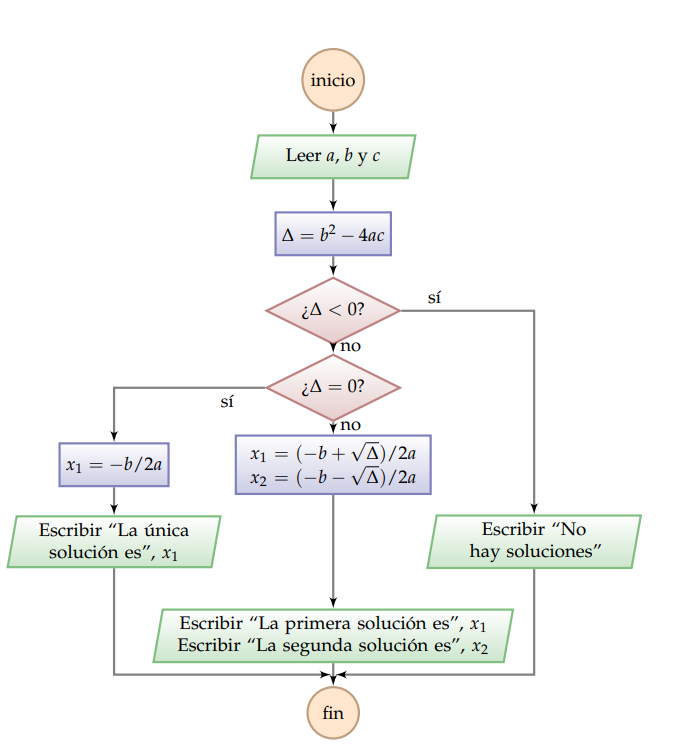
El inicio y el final del algoritmo son representados con bloques circulares. El algoritmo siempre debe ser capaz llegar desde uno hasta el otro, sin importar por qué camino lo hace. Un algoritmo no puede «quedarse pegado» en la mitad.
La entrada y la salida de datos son representadas con romboides, que en la figura de arriba están pintados de verde.
Los diamantes representan condiciones en las que el algoritmo sigue uno de dos caminos. que están etiquetados con sí o no, dependiendo si la condición es verdadera o falsa.
También puede haber ciclos, representados por flechas que regresan a bloques anteriores. En este ejemplo, no hay ciclos.
Otras sentencias van dentro de rectángulos, que en la figura están pintados de azul. En este ejemplo, las sentencias son asignaciones, representadas en la forma nombre = valor.
Los diagramas de flujo no son usados en la práctica para programar, pero son útiles para ilustrar cómo funcionan algoritmos sencillos.
Pseudocódigo
El pseudocódigo es una descripción estructurada de un algoritmo basada en ciertas convenciones notacionales. Si bien es muy parecido al código que finalmente se escribirá en el computador, el pseudocódigo está pensado para ser leído por humanos.
Una manera de escribir el algoritmo para la ecuación cuadrática en pseudocódigo es la siguiente:
leer a
leer b
leer c
discriminante = b² - 4ac
si discriminante < 0:
escribir 'La ecuación no tiene soluciones reales'
o si no, si discriminante = 0:
x = -b / 2a
escribir 'La solución única es', x
o si no:
x1 = (-b - √discriminante) / 2a
x2 = (-b + √discriminante) / 2a
escribir 'Las dos soluciones reales son:'
escribir x1
escribir x2
Las líneas que comienzan con leer y escribir denotan, respectivamente, la entrada y la salida del programa. Los diferentes casos son representados usando sentencias si y o si no. Las asignaciones siguen la misma notación que en el caso de los diagramas de flujo.
La notación de pseudocódigo es bien liberal. Uno puede mezclar notación de matemáticas con frases en español, siempre que quede absolutamente claro para el lector qué representa cada una de las líneas del algoritmo.
Código
El producto final de la programación siempre debe ser código que pueda ser ejecutado en el computador. Esto requiere describir los algoritmos en un lenguaje de programación. Los lenguajes de programación definen un conjunto limitado de conceptos básicos, en función de los cuales uno puede expresar cualquier algoritmo.
En esta asignatura, usaremos el lenguaje de programación Python para escribir nuestros programas.
El código en Python para resolver la ecuación cuadrática es el siguiente:
a = float(raw_input('Ingrese a: '))
b = float(raw_input('Ingrese b: '))
c = float(raw_input('Ingrese c: '))
discriminante = b ** 2 - 4 * a * c
if discriminante < 0:
print 'La ecuacion no tiene soluciones reales'
elif discriminante == 0:
x = -b / (2 * a)
print 'La solucion unica es x =', x
else:
x1 = (-b - (discriminante ** 0.5)) / (2 * a)
x2 = (-b + (discriminante ** 0.5)) / (2 * a)
print 'Las dos soluciones reales son:'
print 'x1 =', x1
print 'x2 =', x2
raw_input()
A partir de ahora, usted aprenderá a entender, escribir y ejecutar códigos como éste.